【题目】某商场经销一种水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现, 在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)当每千克涨价为多少元时,每天的盈利最多?最多是多少?
(2)若商场只要求保证每天的盈利为6000元,同时又可使顾客得到实惠,每千克应涨价为多少?
参考答案:
【答案】(1) ![]() ,6125 元;(2)5元
,6125 元;(2)5元
【解析】试题分析:(1)设每千克涨价x元,利润为y元,根据等量关系“总利润=每千克利润×数量”,列出关系式,求出y与x之间的函数关系,利用二次函数的性质即可求出结论;(2)把y=6000代入(1)的解析式,根据题意使顾客得到实惠就可以得出结论.
试题解析:
(1) 设每千克涨价x元,获利y元 则
y=(10+x)(500-20x)
=-20x+300x+5000
=-20(x-15x)+5000
=-20[x-15x+(![]() )-
)-![]() ]+5000
]+5000
=-20(x-![]() )+1125+5000
)+1125+5000
=-20(x-![]() )+6125
)+6125
因-20<0,抛物线开口向下,
∴当x=7.5时,y最大值=6125.
(2) 当y=6000时,
(10+x)(500-20x)=6000
解方程可得 x1=10,x2=5
要让顾客得到实惠,就是要价格最低,所以每千克应涨价5元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与直线
与直线 交于点O(0,0),A(
交于点O(0,0),A( ,12),点B是抛物线上O,A之间的一个动点,过点B分别作
,12),点B是抛物线上O,A之间的一个动点,过点B分别作 轴、
轴、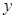 轴的平行线与直线OA交于点C,E.
轴的平行线与直线OA交于点C,E.
(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(
 ,
, ),求出
),求出 ,
, 之间的关系式.
之间的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a2)4(﹣a)3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图用点A(3,1)表示放置3个胡萝卜、1棵青菜,点B(2,3)表示放置2个胡萝卜、3棵青菜.

(1)请你写出其他各点C,D,E,F所表示的意义;
(2)若一只兔子从A到达B(顺着方格线走),有以下几条路可以选择:①A→C→D→B;②A→F→D→B;③A→F→E→B,帮可爱的小白兔选一条路,使它吃到的食物最多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小李在一次高尔夫球选拔赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大水平高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30o,O、A两点相距8
 米.
米.
(1)求直线OA的解析式;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小李这一杆能否把高尔夫球从O点直接打入球洞A点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)a3a2a4+(﹣a)2;
(2)(x2﹣2xy+x)÷x
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(-1,0).设t=a+b+1,则t值的变化范围是( )

A. 0<t<1 B. 0<t<2 C. 1<t<2 D. -1<t<1
相关试题

