【题目】已知,如图:在△ABC中,AC=3,BC=6,∠C=60![]() ;
;
(1)将△ABC绕着点C旋转,使点A落在直线BC上的点A′,点B落在B′,在下图中画出旋转后的△A′B′C.
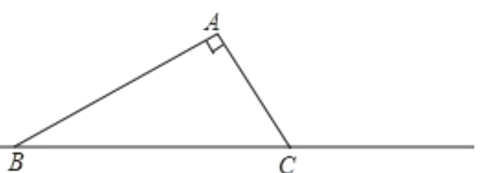
(2)直接写出A′B的长,A′B=___________.
参考答案:
【答案】(1)见详解;(2)3cm或9cm
【解析】
(1)利用∠C=60°和旋转的性质,将△ABC绕着点C顺时针旋转120°时,点A落在直线BC上的点A′,画出此时的△A′B′C;将△ABC绕着点C逆时针旋转60°时,点A落在直线BC上的点A′,画出此时的△A′B′C;
(2)利用(1)中的两个图形分类计算.
解:(1)如图1,如图2,△A′B′C为所作;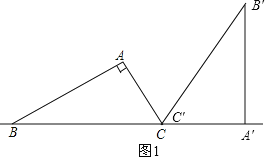
(2)将△ABC绕着点C顺时针旋转120°得到△A′B′C′,如图1,则CA′=CA=3cm,∴A′B=CB+CA′=9cm;
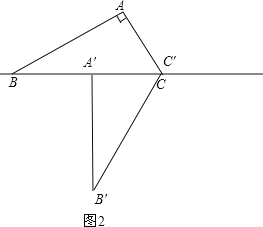
将△ABC绕着点C逆时针旋转60°得到△A′B′C′,如图2,则CA′=CA=3cm,
∴A′B=CB-CA′=3cm.
故A′B为3cm或9cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

-
科目: 来源: 题型:
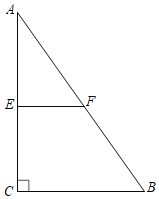
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.
(1)求∠A的度数;
(2)求EF和AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在ABCD中,对角线AC,BD相交于点0,添加下列条件后,能使ABCD成为矩形的是( )
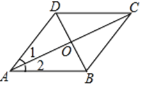
A. AB=ADB. AC=BDC. BD平分∠ABCD. AC⊥BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】若将边长为 a 、b 的正方形 ABCD 按图 ① 中的比例进行分割,可以拼成一个长方形A1 B1C1D1 不重叠、无缝隙),如图②所示.
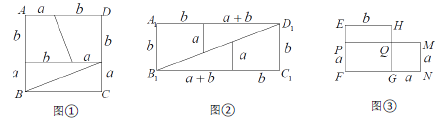
(1)根据图①可以拼成图②的面积关系,请写出 a 、b 之间存在的关系式;
(2)已知图③中,四边形 QMNG 与四边形EFGH 分别是以 a 、b 长为边的正方形与图①中的 a 、b 相同),在图 3 已有的四边形中,面积相等的四边形有几组?请分别写出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校120名学生某一周用于阅读课外书籍的时间的频率分布直方图如图所示.其中阅读时间是8~10小时的频数和频率分别是( )
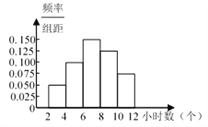
A. 15和0.125 B. 15和0.25 C. 30和0.125 D. 30和0.25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1的圆O1与半径为3的圆O2相内切,如果半径为2的圆与圆O1和圆O2都相切,那么这样的圆的个数是 ( )
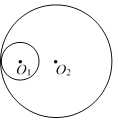
A. 1 B. 2 C. 3 D. 4
相关试题

