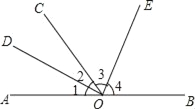
【题目】如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,OD⊥OE,垂足为点O.
(1)求∠BOD的度数;
(2)说明OE平分∠BOC.
参考答案:
【答案】(1)154°;(2)OE平分∠BOC.理由见解析.
【解析】
(1)根据角平分线的定义得到∠1的度数,再利用邻补角的定义即可得到结论;
(2)分别求得∠3与∠4的度数即可说明.
(1)∵∠AOC=52°,OD平分∠AOC,∴∠1==∠2=![]() ∠AOC=26°,∴∠BOD=180°-∠1=154°;
∠AOC=26°,∴∠BOD=180°-∠1=154°;
(2)OE平分∠BOC.理由如下:
∵OD⊥OE,∴∠DOE=90°.
∵∠DOC=26°,∴∠3=∠DOE﹣∠2=90°﹣26°=64°.
又∵∠4=∠BOD﹣∠DOE=154°﹣90°=64°,∴∠3=∠4,∴OE平分∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3
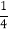 ﹣5
﹣5 ﹣(﹣1
﹣(﹣1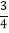 )﹣3
)﹣3 +12
+12 ﹣(﹣12
﹣(﹣12 )
)(2)|﹣
 |×[﹣32÷(﹣
|×[﹣32÷(﹣ )2+(﹣2)3]
)2+(﹣2)3](3)先化简,再求值:2x2﹣[3(﹣
 x2+
x2+ xy)﹣2y2]﹣2(x2﹣xy+2y2),其中x、y满足|x﹣
xy)﹣2y2]﹣2(x2﹣xy+2y2),其中x、y满足|x﹣ |+(y+1)2=0.
|+(y+1)2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.


图1 图2
-
科目: 来源: 题型:
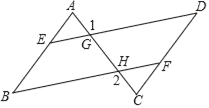
查看答案和解析>>【题目】在括号内注明说理依据.如图已知∠B=∠D,∠1=∠2,试猜想∠A与∠C的大小关系,并说明理由.
解:猜想∠A=∠C
∵∠1=∠2 (已知)
∠1=∠EGC
∴∠2=∠EGC
∴BF∥DE
∴∠B=∠AED
∵∠B=∠D
∴∠AED=∠D (等量代换)
∴AB∥CD
∴∠A=∠C .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市公租房倍受社会关注,2012年竣工的公租房有A,B,C,D 四种型号共500套,B型号公租房的入住率为40%.A,B,C,D 四种型号竣工的套数及入住的情况绘制了图1和图2两幅尚不完整的统计图.

(1)请你将图1和图2的统计图补充完整;
(2)在安置中,由于D型号公租房很受欢迎,入住率很高,2012年竣工的D型公租房中,仅有5套没有入住,其中有两套在同一单元同一楼层,其余3套在不同的单元不同的楼层.老王和老张分别从5套中各任抽1套,用树状图或列表法求出老王和老张住在同一单元同一楼层的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )

A. 88° B. 30° C. 32° D. 48°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.

(1)求证:△BOE≌△DOF;
(2)若OA= BD,则四边形ABCD是什么特殊四边形?请说明理由.
BD,则四边形ABCD是什么特殊四边形?请说明理由.
相关试题

