【题目】计算:
(1)3![]() ﹣5
﹣5![]() ﹣(﹣1
﹣(﹣1![]() )﹣3
)﹣3![]() +12
+12![]() ﹣(﹣12
﹣(﹣12![]() )
)
(2)|﹣![]() |×[﹣32÷(﹣
|×[﹣32÷(﹣![]() )2+(﹣2)3]
)2+(﹣2)3]
(3)先化简,再求值:2x2﹣[3(﹣![]() x2+
x2+![]() xy)﹣2y2]﹣2(x2﹣xy+2y2),其中x、y满足|x﹣
xy)﹣2y2]﹣2(x2﹣xy+2y2),其中x、y满足|x﹣![]() |+(y+1)2=0.
|+(y+1)2=0.
参考答案:
【答案】(1)21;(2)﹣18;(3)x2﹣2y2,原式=﹣![]() .
.
【解析】
(1)直接根据有理数加减法法则和加法交换律计算得出答案;
(2)直接利用有理数的混合运算法则计算得出答案;
(3)首先去括号,进而合并同类项,再利用非负数的性质求出x,y的值,代入即可得出答案.
(1)原式=3![]() ﹣5
﹣5![]() +1
+1![]() ﹣3
﹣3![]() +12
+12![]() +12
+12![]()
=3![]() ﹣5
﹣5![]() ﹣3
﹣3![]() +12
+12![]() +12
+12![]()
=5﹣9+25
=21;
(2)原式=![]() ×[﹣9×
×[﹣9×![]() ﹣8]
﹣8]
=![]() ×[﹣4﹣8]
×[﹣4﹣8]
=![]() ×(﹣12)
×(﹣12)
=﹣18;
(3)原式=2x2﹣(﹣x2+2xy﹣2y2)﹣2x2+2xy﹣4y2
=2x2+x2﹣2xy+2y2﹣2x2+2xy﹣4y2
=x2﹣2y2
∵|x﹣![]() |+(y+1)2=0,∴x=
|+(y+1)2=0,∴x=![]() ,y=﹣1.
,y=﹣1.
当x=![]() ,y=﹣1时,原式=(
,y=﹣1时,原式=(![]() )2﹣2×(﹣1)2=﹣
)2﹣2×(﹣1)2=﹣![]() .
.
-
科目: 来源: 题型:
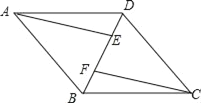
查看答案和解析>>【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:|m|=2,a,b互为相反数,且都不为零,c,d互为倒数.则2a+2b+(
 ﹣3cd)﹣m的值是_____.
﹣3cd)﹣m的值是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A1 , A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1 , A3B2∥A2B1 , A3B3∥A2B2 , A4B3∥A3B2 , ….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.


图1 图2
-
科目: 来源: 题型:
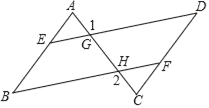
查看答案和解析>>【题目】在括号内注明说理依据.如图已知∠B=∠D,∠1=∠2,试猜想∠A与∠C的大小关系,并说明理由.
解:猜想∠A=∠C
∵∠1=∠2 (已知)
∠1=∠EGC
∴∠2=∠EGC
∴BF∥DE
∴∠B=∠AED
∵∠B=∠D
∴∠AED=∠D (等量代换)
∴AB∥CD
∴∠A=∠C .
-
科目: 来源: 题型:
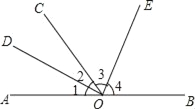
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,OD⊥OE,垂足为点O.
(1)求∠BOD的度数;
(2)说明OE平分∠BOC.
相关试题

