【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

参考答案:
【答案】(1)A点坐标是(2,3);(2)![]() =
=![]() ;(3)P点坐标是(0,
;(3)P点坐标是(0, ![]() );(4)点Q是坐标是(
);(4)点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).
【解析】
解析
联立方程,解方程即可求得;
C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(![]() ,0),由(1)得A点坐标,可得
,0),由(1)得A点坐标,可得![]() 的值;
的值;
(3)设P点坐标是(0,y),根据勾股定理列出方程,解方程即可求得;
(4)分两种情况:①当Q点在线段AB上:作QD⊥y轴于点D,则QD=x,根据
![]() =
=![]() -
-![]() 列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=-y,根据
列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=-y,根据![]() =
=![]() -
- ![]() 列出关于y的方程解方程求得即可.
列出关于y的方程解方程求得即可.
解(1)解方程组: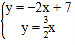 得:
得:![]() ,
,
![]() A点坐标是(2,3);
A点坐标是(2,3);
(2)![]() C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(
C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(![]() ,0)
,0)
![]()
![]() =
=![]() =
=![]()
(3)设P点坐标是(0,y ),
![]() △OAP是以OA为底边的等腰三角形,
△OAP是以OA为底边的等腰三角形,
![]() OP=PA,
OP=PA,
![]()
![]() ,
,
解得y=![]() ,
,
![]() P点坐标是(0,
P点坐标是(0, ![]() ),
),
故答案为(0, ![]() );
);
(4)存在;
由直线y=-2x+7可知B(0,7),C(![]() ,0),
,0),
![]()
![]() =
=![]() =
=![]() <6,
<6,
![]() =
=![]() =7>6,
=7>6,
![]() Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
当Q点在线段AB上:作QD⊥y轴于点D,如图1, 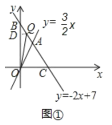
则QD=x,![]()
![]() =
=![]() -
-![]() =7-6=1,
=7-6=1,
![]()
![]() OB
OB![]() QD=1,即:
QD=1,即: ![]()
![]() 7x=1,
7x=1,
![]() x=
x=![]() ,
,
把x=![]() 代入y=-2x+7,得y=
代入y=-2x+7,得y=![]() ,
,
![]() Q的坐标是(
Q的坐标是(![]() ,
,![]() ),
),
当Q点在AC的延长线上时,作QD⊥x轴于点D,如图2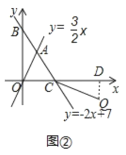
则QD=-y,
![]()
![]() =
=![]() -
- ![]() =6-
=6-![]() =
=![]() ,
,
![]()
![]() OC
OC![]() QD=
QD=![]() ,即:
,即:![]() ,
,
![]() y=-
y=-![]() ,
,
把y=-![]() 代入y=-2x+7,解得x=
代入y=-2x+7,解得x=![]()
![]() Q的坐标是(
Q的坐标是(![]() ,-
,-![]() ),
),
综上所述:点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=10,BC=16.点D在边BC上,且点D到边AB和边AC的距离相等.
(1)用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上标注出点D);
(2)求点D到边AB的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1 , y2 , y3的大小关系为( )
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y3>y1>y2 -
科目: 来源: 题型:
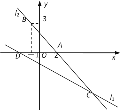
查看答案和解析>>【题目】如图,直线l1的函数关系式为y=-
 x-1,且l1与x轴交于点D,直线l2经过点A(2,0),B(-1,3),直线l1与l2交于点C.
x-1,且l1与x轴交于点D,直线l2经过点A(2,0),B(-1,3),直线l1与l2交于点C.(1)求直线l2的函数关系式;
(2)点C的坐标为 ;
(3)求△ADC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D落在点H的位置上,点C恰好落在边AD上的点G处,连接EG.
(1)△GEF是等腰三角形吗?请说明理由;
(2)若CD=4,GD=8,求HF的长度.
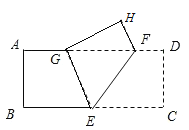
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5a2b÷
 ×2ab2;
×2ab2;(2)[(x+2y)2-(x+y)(x-y)-5y2]÷2x;
(3)(-3.6×1010)÷(-2×102)2;
(4)(2a-b+3)(2a-3+b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E.
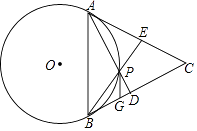
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数.
相关试题

