搜索
【题目】∠COD=36°19′，下列正确的是（ ）
A.∠COD=36.19°B.∠COD的补角为144°41′C.∠COD的余角为53°19′ D.∠COD的余角为53°41′
参考答案：
【答案】D
【解析】
根据角度的换算及补角、余角的定义即可逐一判断．
解：∠COD=36°19′≈36.301°，故A错误；
∠COD的补角为143°41′，故B错误；
∠COD的余角为53°41′，故C错误，D正确；
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知点A（3，2），AC⊥x轴，垂足为点C，则点C的坐标为_________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，码头A、B分别在海岛O的北偏东45°和北偏东60°方向上，仓库C在海岛O的北偏东75°方向上，码头A、B均在仓库C的正西方向，码头B和仓库C的距离BC=50km，若将一批物资从仓库C用汽车运送到A、B两个码头中的一处，再用货船运送到海岛O，若汽车的行驶速度为50km/h，货船航行的速度为25km/h，问这批物资在哪个码头装船，最早运抵海岛O？（两个码头物资装船所用的时间相同，参考数据：
≈1.4， 
≈1.7）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，∠A=∠C=90°，BE，DF分别是∠ABC，∠ADC的平分线．
（1）∠1与∠2有什么关系，为什么？
（2）BE与DF有什么关系？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】-27的立方根与81的算术平方根的和是___________．
-
科目： 来源： 题型：
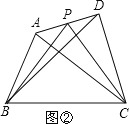
查看答案和解析>>【题目】提出问题：如图①，在四边形ABCD中，P是AD边上任意一点，
△PBC与△ABC和△DBC的面积之间有什么关系？
探究发现：为了解决这个问题，我们可以先从一些简单的、特殊的情形入手：
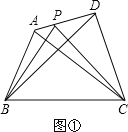
（1）当AP=
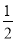AD时（如图②）：∵AP=
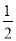AD，△ABP和△ABD的高相等，∴S△ABP=
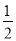S△ABD．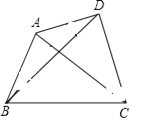
∵PD=AD﹣AP=
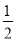AD，△CDP和△CDA的高相等，∴S△CDP=
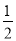S△CDA．∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP
=S四边形ABCD﹣
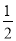S△ABD﹣
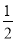S△CDA=S四边形ABCD﹣
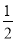（S四边形ABCD﹣S△DBC）﹣
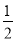（S四边形ABCD﹣S△ABC）=
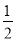S△DBC+
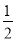S△ABC．（2）当AP=
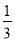AD时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；（3）当AP=
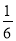AD时，S△PBC与S△ABC和S△DBC之间的关系式为： ；（4）一般地，当AP=
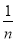AD（n表示正整数）时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；问题解决：当AP=
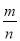AD（0≤
≤1）时，S△PBC与S△ABC和S△DBC之间的关系式为： ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，在Rt△ABC中，∠ACB=90°，AE平分∠BAC交BC于点E，D为AC上的点，BE=DE．
（1）求证：∠B+∠EDA=180°；
（2）求
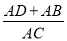的值．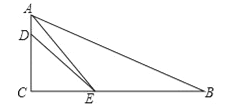
相关试题
