【题目】如图1,在同一平面内,四条线AB、BC、CD、DA首尾顺次相接,AD、BC相交于点O,AM、CN分别是∠BAD和∠BCD的平分线,∠B=α,∠D=β.

(1)如图2,AM、CN相交于点P.
①当α=β时,判断∠APC与α的大小关系,并说明理由.
②当α>β时,请直接写出∠APC与α,β的数量关系.
(2)是否存在AM∥CN的情况?若存在,请判断并说明α,β的数量关系;若不存在,请说明理由.
参考答案:
【答案】(1)①当α=β时,∠APC=α.理由见解析;②当α>β时,∠APC=![]() (α+β);
(α+β);
(2)不存在.理由见解析.
【解析】
(1)①当α=β时,根据三角形内角和定理得∠2+∠D=∠4+∠APC,∠OCD+∠D=∠B+∠OAB,则∠OCD=∠OAB,根据角平分线定义得∠2=∠4,所以∠APC=∠D=α;②∠2+∠D=∠4+∠APC,∠OCD+∠D=∠B+∠OAB,则∠2+β=∠4+∠APC,2∠2+β=α+2∠4,所以∠APC=![]() (α+β);
(α+β);
(2)若AM∥CN,则∠4=∠5,由∠5=∠2+∠D得到∠4=∠2+β,同理得∠3=∠1+α,然后把两等式相加得到α+β=0,由此判断不存在AM∥CN.
(1)如图2,
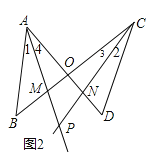
①当α=β时,∠APC=α.理由如下:
在△ANP和△CND中,∠2+∠D=∠4+∠APC,
在△AOB和△COD中,∠OCD+∠D=∠B+∠OAB,
∵∠D=∠B=α,
∴∠OCD=∠OAB,
∵AM、CN分别是∠BAD和∠BCD的平分线,
∴∠OCD=2∠2,∠OAB=2∠4,
∴∠2=∠4,
∴∠APC=∠D=α;
②当α>β时,∠APC=![]() (α+β);
(α+β);
∵∠2+∠D=∠4+∠APC,∠OCD+∠D=∠B+∠OAB,
∴∠2+β=∠4+∠APC,2∠2+β=α+2∠4,
∴∠APC=∠2-∠4+β,∠2-∠4=![]() α-
α-![]() β
β
∴∠APC=![]() α-
α-![]() β+β=
β+β=![]() α+
α+![]() β,
β,
所以∠APC=![]() (α+β);
(α+β);
(2)不存在.理由如下:
如图1,
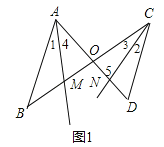
若AM∥CN,则∠4=∠5,
∵∠5=∠2+∠D,
∴∠4=∠2+β,
同理得∠3=∠1+∠B,即∠3=∠1+α,
∴∠3+∠4=∠1+∠2+α+β,
∵AM、CN分别是∠BAD和∠BCD的平分线,
∴∠3=∠2,∠1=∠4,
∴α+β=0,
∴不存在AM∥CN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC的三边长分别为m﹣2,2m+1,8.
(1)试确定m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长;
(3)若△ABC为等腰三角形,试确定另外两边的长.
-
科目: 来源: 题型:
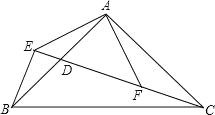
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 轴、
轴、 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线 相交于点A.
相交于点A.(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线
 上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,BC=2,AC=4,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
(1)若PD⊥AB,求AP.
(2)当AD=PE时,求证:四边形BDEP为菱形.
(3)若△PDE与△ABC重合部分的面积等于△PAB面积的
 ,求AP.
,求AP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 经过点A(
经过点A( ,0),B(
,0),B( ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一张三角形纸片ABC,其中∠BAC=60°,BC=6,点D是BC边上一动点,将BD,CD翻折使得B′,C′分别落在AB,AC边上,(B与B′,C与C′分别对应),点D从点B运动至点C,△B′C′D面积的大小变化情况是( )

A. 一直减小 B. 一直不变 C. 先减小后增大 D. 先增大后减小
相关试题

