【题目】若△ABC的三边长分别为m﹣2,2m+1,8.
(1)试确定m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长;
(3)若△ABC为等腰三角形,试确定另外两边的长.
参考答案:
【答案】(1)3<m<5;(2)△ABC的周长=19;(3)另外两边的长为![]() 和8.
和8.
【解析】
(1)根据三角形的三边关系,可得①(m-2)+(2m+1)>8,(2m+1)-(m-2)<8,解①②组成的不等式组可得;
(2)根据题意和m的取值,即可得出m=4,从而得出边的长,三边相加即可求得三角形的周长;
(3)分三种情况分别讨论即可求得m=![]() ,代入m-2,2m+1即可求得另外两边的长.
,代入m-2,2m+1即可求得另外两边的长.
(1)根据三角形的三边关系得
![]() ,
,
解得3<m<5;
(2)∵△ABC的三边均为整数,
∴m=4,
∴△ABC的周长=m﹣2+2m+1+8=19;
(3)当m﹣2=2m+1时,
解得m=﹣3(不合题意,舍去),
当m﹣2=8时,
解得,m=10>5(不合题意,舍去),
当2m+1=8时,
解得,m=![]() ,
,
所以若△ABC为等腰三角形,m=![]() ,
,
则m﹣2=![]() ,2m+1=8,
,2m+1=8,
所以,另外两边的长为![]() 和8.
和8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O直径,点C在⊙O上,
AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.
(1)求证:BD=BE;
(2)若DE=2,BD=
 ,求CE的长.
,求CE的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的平分线交于点D1,∠ABD1与∠ACD1的平分线交于点D2,以此类推,∠ABD2与∠ACD2的平分线交于点D,则∠BDC的度数是__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10的网格中,已知A(0,4),B(﹣2,2),C(3,0).

(1)在如图网格中画出△ABC,及△ABC关于x轴对称的△A1B1C1;
(2)写出点A1、B1、C1的坐标.
(3)求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.
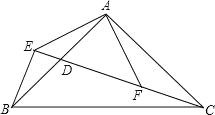
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 轴、
轴、 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线 相交于点A.
相交于点A.(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线
 上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在同一平面内,四条线AB、BC、CD、DA首尾顺次相接,AD、BC相交于点O,AM、CN分别是∠BAD和∠BCD的平分线,∠B=α,∠D=β.

(1)如图2,AM、CN相交于点P.
①当α=β时,判断∠APC与α的大小关系,并说明理由.
②当α>β时,请直接写出∠APC与α,β的数量关系.
(2)是否存在AM∥CN的情况?若存在,请判断并说明α,β的数量关系;若不存在,请说明理由.
相关试题

