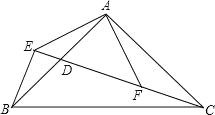
【题目】在Rt△ABC中,BC=2,AC=4,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
(1)若PD⊥AB,求AP.
(2)当AD=PE时,求证:四边形BDEP为菱形.
(3)若△PDE与△ABC重合部分的面积等于△PAB面积的![]() ,求AP.
,求AP.

参考答案:
【答案】(1)![]() ;(2)见解析:(3) AP=3或
;(2)见解析:(3) AP=3或![]() .
.
【解析】
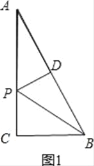
(1)如图1,根据勾股定理可求出AB,从而得到AD、BD的值,易证△ADP∽△ACB,只需运用相似三角形的性质就可求出AP的值;
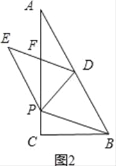
(2)由折叠可得:PE=PB,DE=DB,又有AD=PE,AD=DB,从而PE=PB=DB=DE,然后根据四条边相等的四边形形是菱形即可证明四边形BDEP为菱形;
(3)根据条件可得S△PDF=![]() S△PAB=
S△PAB=![]() S△ADP=
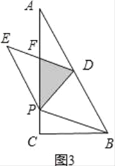
S△ADP=![]() S△EDP,从而可得AF=PF,EF=DF.而符合条件的位置有两个(图3、图4),需分两种情况讨论:①如图3,根据三角形中位线定理可得DF∥BP,则有∠EDP=∠BPD.由折叠可得∠BDP=∠EDP,从而可得∠BDP=∠BPD,即可得到BP=BD=2
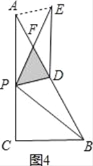
S△EDP,从而可得AF=PF,EF=DF.而符合条件的位置有两个(图3、图4),需分两种情况讨论:①如图3,根据三角形中位线定理可得DF∥BP,则有∠EDP=∠BPD.由折叠可得∠BDP=∠EDP,从而可得∠BDP=∠BPD,即可得到BP=BD=2![]() ,在Rt△BCP中运用勾股定理可求出PC,就可得到AP的值;②如图4,连接AE,由AF=PF,EF=DF可得四边形AEDP是平行四边形,则有AP=ED,由折叠可得DE=DB,即可得到AP=DB=2
,在Rt△BCP中运用勾股定理可求出PC,就可得到AP的值;②如图4,连接AE,由AF=PF,EF=DF可得四边形AEDP是平行四边形,则有AP=ED,由折叠可得DE=DB,即可得到AP=DB=2![]() .
.
解:(1)如图1,
∵∠C=90°,BC=2,AC=4,
∴AB=![]() =2
=2![]() .
.
∵点D为AB的中点,
∴AD=BD=![]() .
.
∵PD⊥AB,
∴∠ADP=90°.
∵∠A=∠A,∠ADP=∠C,
∴△ADP∽△ACB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AP=![]() ;
;
(2)证明:如图2,
由折叠可得:PE=PB,DE=DB.
∵AD=PE,AD=DB,
∴PE=PB=DB=DE,
∴四边形BDEP为菱形;
(3)∵点D是线段AB的中点,
∴S△ADP=S△BDP=![]() S△PAB.
S△PAB.
由折叠可得:S△EDP=S△BDP,
∴S△PDF=![]() S△PAB=
S△PAB=![]() S△ADP=
S△ADP=![]() S△EDP,
S△EDP,
∴AF=PF,EF=DF.
①如图3,
根据三角形中位线定理可得:DF∥BP,
∴∠EDP=∠BPD.
由折叠可得∠BDP=∠EDP,
∴∠BDP=∠BPD,
∴BP=BD=![]() ,
,
∴PC=![]() =
=![]() =1,
=1,
∴AP=4﹣1=3;
②如图4,
连接AE,
∵AF=DF,EF=PF,
∴四边形AEDP是平行四边形,
∴AP=ED,
由折叠可得:DE=DB,
∴AP=DB=![]() .
.
综上所述:AP=3或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 轴、
轴、 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线 相交于点A.
相交于点A.(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线
 上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在同一平面内,四条线AB、BC、CD、DA首尾顺次相接,AD、BC相交于点O,AM、CN分别是∠BAD和∠BCD的平分线,∠B=α,∠D=β.

(1)如图2,AM、CN相交于点P.
①当α=β时,判断∠APC与α的大小关系,并说明理由.
②当α>β时,请直接写出∠APC与α,β的数量关系.
(2)是否存在AM∥CN的情况?若存在,请判断并说明α,β的数量关系;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 经过点A(
经过点A( ,0),B(
,0),B( ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一张三角形纸片ABC,其中∠BAC=60°,BC=6,点D是BC边上一动点,将BD,CD翻折使得B′,C′分别落在AB,AC边上,(B与B′,C与C′分别对应),点D从点B运动至点C,△B′C′D面积的大小变化情况是( )

A. 一直减小 B. 一直不变 C. 先减小后增大 D. 先增大后减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】设m是不小于﹣1的实数,关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x1、x2,
(1)若x12+x22=6,求m值;
(2)令T=
 ,求T的取值范围.
,求T的取值范围.
相关试题

