【题目】如图,已知一次函数y=kx+b (k≠0) 的图像与反比例函数y=-![]() 的图像交于A(-2,m)和B (n,-2) 两点,求:(1)一次函数的解析式;
的图像交于A(-2,m)和B (n,-2) 两点,求:(1)一次函数的解析式;
(2)△AOB的面积.

参考答案:
【答案】(1)y= -x+2;(2)6.
【解析】
(1)先把A的横坐标和B点的纵坐标分别代入y=-![]() ,可确定点A的坐标为(-2,4),B点坐标为(4,-2),然后利用待定系数法可求出一次函数的解析式;
,可确定点A的坐标为(-2,4),B点坐标为(4,-2),然后利用待定系数法可求出一次函数的解析式;
(2)先确定次函数与y轴的交点坐标,然后利用S△AOB=S△AOC+S△BOC进行计算即可.
解:(1)把(-2,m)代入y=![]() 得m=4,把(n,-2)代入y=
得m=4,把(n,-2)代入y=![]() 得n=4,
得n=4,
∴点A的坐标为(2,4),B点坐标为(4,2),
把A(2,4),B(4,2)分别代入y=kx+b得
![]() ,解得
,解得![]() ,
,
∴一次函数的解析式为y=x+2;
(2)如图,直线AB交y轴于点C,
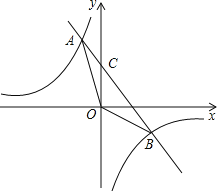
对于y=x+2,令x=0,则y=2,则C点坐标为(0,2),
∴S△AOB=S△AOC+S△BOC=![]() ×2×2+
×2×2+![]() ×2×4=6.
×2×4=6.
故答案为:(1)y= -x+2;(2)6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p,x1·x2=q.请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0 (n≠0),求出一个一元二次方程,使它的两根分别是已知方程两根的倒数;
(2)已知a、b满足a2-15a-5=0,b2-15b-5=0,求
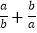 的值;
的值;(3)已知a、b、c均为实数,且a+b+c=0,abc=16,求正数c的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在武胜县中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生棵根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.

请你结合图中信息,解答下列问题:
(1)本次共调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的有 人,表示最喜爱甲类图书的人数扇形的圆心角的度数是 ;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的
 倍,若这所学校共有学生
倍,若这所学校共有学生 人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,四边形ABCD中,∠A=106°
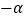 , ∠ABC=74°
, ∠ABC=74°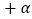 ,BD⊥DC于点D, EF⊥DC于点F.
,BD⊥DC于点D, EF⊥DC于点F.求证:∠1=∠2.

证明: ∵∠A=106°
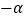 ,∠ABC=74°
,∠ABC=74°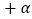 (已知)
(已知)∴∠A+∠ABC=180°
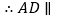 ( )
( )∴∠1=
∵BD⊥DC,EF⊥DC (已知)
∴∠BDF=∠EFC=90°( )
∴BD∥ ( )
∴∠2= ( )
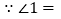 (已证)
(已证)∴∠1=∠2 ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】广安某大型蔬菜超市从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种
西红柿
青椒
西兰花
豆角
批发价(元/
 )
)3.6
5.4
8
4.8
零售价(元/
 )
)5.4
8.4
14
7.6
请解答下列问题:
(1)第一天,该蔬菜超市批发青椒和豆角两种蔬菜共
 ,用去了
,用去了 元钱,问该蔬菜超市批发青椒和豆角两种蔬菜各多少千克?
元钱,问该蔬菜超市批发青椒和豆角两种蔬菜各多少千克?(2)在(1)的条件,这两种蔬菜当天全部售完一共能盈利多少?
(3)第二天,蔬菜超市用
 元钱批发青椒和西兰花,要想当天全部售完后所盈利不少于
元钱批发青椒和西兰花,要想当天全部售完后所盈利不少于 元,则该经营户最多能批发青椒多少?(结果取整数)
元,则该经营户最多能批发青椒多少?(结果取整数) -
科目: 来源: 题型:
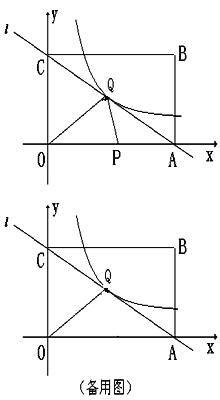
查看答案和解析>>【题目】已知,长方形OABC在平面直角坐标系内的位置如图所示,点O为坐标原点,点A的坐标为(10,0),点B的坐标为(10,8).
(1)直接写出点C的坐标为:C( , );
(2)已知直线AC与双曲线y=
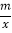 (m≠0)在第一象限内有一点交点Q为(5,n);
(m≠0)在第一象限内有一点交点Q为(5,n);①求m及n的值;
②若动点P从A点出发,沿折线AO→OC的路径以每秒2个单位长度的速度运动,到达C处停止.求△OPQ的面积S与点P的运动时间t(秒)的函数关系式.
相关试题

