【题目】在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(0,4),点M是线段AB上任意一点(A,B两点除外)。
(1)求直线AB的解析式;
(2)过点M分别作MC⊥OA于点C,MD⊥OB于点D,当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(3)当点M把线段AB分成的两部分的比为1:3时,请求出点M的坐标。

参考答案:
【答案】(1)AB的解析式为![]() .(2)不发生变化;理由见解析;(3)M(1,3)或M(3,1)
.(2)不发生变化;理由见解析;(3)M(1,3)或M(3,1)
【解析】(1)设直线AB的解析式为![]() ,
,
则![]()
解得: ![]()
所以AB的解析式为![]() .
.
(2)不发生变化;理由如下:
设M点的坐标为(![]() ,
, ![]() )
)
MD= ![]() , MC=
, MC=![]()
四边形OCMD的周长=2(MD+MC)=![]()
所以四边形OCMD的周长不发生变化.
(3)∵DM∥x轴
∴![]()
①当BM:MA=1:3时,![]() ,即
,即![]() ,DM=1,则点M的横坐标为1,此时纵坐标
,DM=1,则点M的横坐标为1,此时纵坐标![]() ,M(1,3)
,M(1,3)
②当BM:MA=3:1时, ![]() ,即
,即![]() ,DM=3,则点M的横坐标为3,
,DM=3,则点M的横坐标为3,
此时纵坐标![]() ,M(3,1)
,M(3,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
 ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )

A. ①② B. ②③ C. ①②④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:
(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出S△ABC与S四边形AFBD的关系
(2)如图2,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△ABC应满足什么条件:请给出证明;
(3)在(2)的条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你画出图形,此时CG与CF有何数量关系.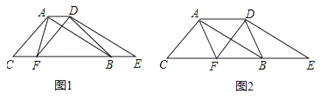
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x2-3=2x+1的二次项系数为________,一次项系数为_________,常数项为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.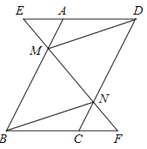
-
科目: 来源: 题型:
查看答案和解析>>【题目】4836′的余角是_________,补角是_________.
-
科目: 来源: 题型:
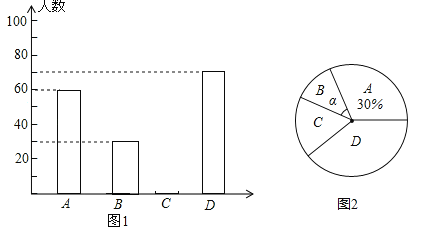
查看答案和解析>>【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
相关试题

