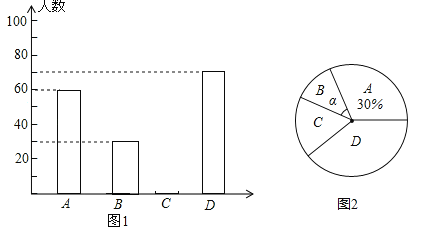
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
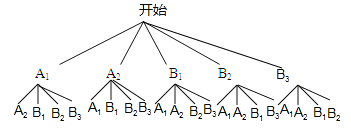
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
参考答案:
【答案】(1)200;(2)C;(3)54°;(4)![]() .
.
【解析】
试题分析:(1)根据B类的人数和所占的百分比即可求出总数;求出C的人数从而补全统计图;
(2)根据中位数定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数可得答案;
(3)用B的人数除以总人数再乘以360°,即可得到圆心角α的度数;
(4)先设甲班学生为A1,A2,乙班学生为B1,B2,B3根据题意画出树形图,再根据概率公式列式计算即可.
试题解析:(1)共调查的中学生数是:80÷40%=200(人),C类的人数是:200﹣60﹣80﹣20=40(人),如图1:

(2)本次抽样调查中,学习时间的中位数落在C等级内;
(3)根据题意得:α=![]() ×360°=54°;
×360°=54°;
(4)设甲班学生为A1,A2,乙班学生为B1,B2,B3,画树状图为:
一共有20种等可能结果,其中2人来自不同班级共有12种,∴P(2人来自不同班级)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(0,4),点M是线段AB上任意一点(A,B两点除外)。
(1)求直线AB的解析式;
(2)过点M分别作MC⊥OA于点C,MD⊥OB于点D,当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(3)当点M把线段AB分成的两部分的比为1:3时,请求出点M的坐标。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.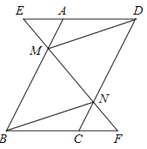
-
科目: 来源: 题型:
查看答案和解析>>【题目】4836′的余角是_________,补角是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)﹣xy2(x+y)3+x(x+y)2的公因式是__;
(2)4x(m﹣n)+8y(n﹣m)2的公因式是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果等腰三角形一腰上的高与另一腰的夹角为45°,那么这个等腰三角形的底角度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,
使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则
∠CMF= .
相关试题

