【题目】如图,两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:
(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出S△ABC与S四边形AFBD的关系
(2)如图2,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△ABC应满足什么条件:请给出证明;
(3)在(2)的条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你画出图形,此时CG与CF有何数量关系.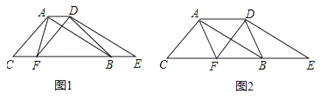
参考答案:
【答案】解:(1)S△ABC=S四边形AFBD ,
理由:由题意可得:AD∥EC,
则S△ADF=S△ABD ,
故S△ACF=S△ADF=S△ABD ,
则S△ABC=S四边形AFBD;
(2)△ABC为等腰直角三角形,即:AB=AC,∠BAC=90°,
理由如下:
∵F为BC的中点,
∴CF=BF,
∵CF=AD,
∴AD=BF,
又∵AD∥BF,
∴四边形AFBD为平行四边形,
∵AB=AC,F为BC的中点,
∴AF⊥BC,
∴平行四边形AFBD为矩形
∵∠BAC=90°,F为BC的中点,
∴AF=![]() BC=BF,
BC=BF,
∴四边形AFBD为正方形;
(3)如图3所示: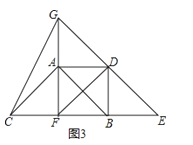
由(2)知,△ABC为等腰直角三角形,AF⊥BC,
设CF=k,则GF=EF=CB=2k,
由勾股定理得:CG=![]() k,
k,
∴CG=![]() CF.
CF.
【解析】(1)利用平行线的性质以及三角形面积关系,得出答案;
(2)利用平行四边形的判定得出四边形AFBD为平行四边形,进而得出AF=![]() BC=BF,求出答案;
BC=BF,求出答案;
(3)根据题意画出图形,设CF=k,利用勾股定理求出即可.
【考点精析】关于本题考查的平行线的性质和勾股定理的概念,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从地面竖直向上抛出一个小球,小球的高度h(米)与运动时间t(秒)之间的关系式为h=30t﹣5t2 , 那么小球抛出秒后达到最高点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小康在小乐的南偏东30°方位,则小乐在小康的( )方位
A. 南偏东30° B. 南偏东60° C. 北偏西30° D. 北偏西60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
 ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )

A. ①② B. ②③ C. ①②④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x2-3=2x+1的二次项系数为________,一次项系数为_________,常数项为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(0,4),点M是线段AB上任意一点(A,B两点除外)。
(1)求直线AB的解析式;
(2)过点M分别作MC⊥OA于点C,MD⊥OB于点D,当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(3)当点M把线段AB分成的两部分的比为1:3时,请求出点M的坐标。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.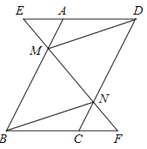
相关试题

