【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.
其中说法正确的是( )

A. ①② B. ②③ C. ①②④ D. ②③④
参考答案:
【答案】C
【解析】试题分析:根据图象得出a>0,b=2a>0,c<0,即可判断①②;把x=2代入抛物线的解析式即可判断③,求出点(﹣5,y1)关于对称轴的对称点的坐标是(3,y1),根据当x>﹣1时,y随x的增大而增大即可判断④.
解:∵二次函数的图象的开口向上,
∴a>0,
∵二次函数的图象y轴的交点在y轴的负半轴上,
∴c<0,
∵二次函数图象的对称轴是直线x=﹣1,
∴﹣![]() =﹣1,
=﹣1,
∴b=2a>0,
∴abc<0,∴①正确;
2a﹣b=2a﹣2a=0,∴②正确;
∵二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).
∴与x轴的另一个交点的坐标是(1,0),
∴把x=2代入y=ax2+bx+c得:y=4a+2b+c>0,∴③错误;
∵二次函数y=ax2+bx+c图象的对称轴为x=﹣1,
∴点(﹣5,y1)关于对称轴的对称点的坐标是(3,y1),
根据当x>﹣1时,y随x的增大而增大,
∵![]() <3,
<3,
∴y2<y1,∴④正确;
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某下岗职工购进一批货物,到集贸市场零售,已知卖出去的货物数量x与售价y的关系如下表:
数量x(千克)
1
2
3
4
5
售价y(元)
3+0.1
6+0.2
9+0.3
12+0.4
15+0.5
写出用x表示y的公式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
(1)根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(2)某人乘坐13km,应付多少钱?
(3)若某人付车费42元,出租车行驶了多少千米?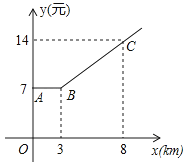
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x+1)2=4(x-2)2的解是( )
A. x=1B. x=5C. x1=1,x2=5D. x1=1,x2=-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列条件,能作出平行四边形的是( )
A. 两组对边的长分别是3和5
B. 相邻两边的长分别是3和5,且一条对角线长为9
C. 一边的长为7,两条对角线的长分别为6和8
D. 一边的长为7,两条对角线的长分别为6和5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数
 与
与 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程 的两个根.
的两个根. (1)请直接写出点A、B的坐标,并求出该二次函数的解析式.
(2)如图1,在二次函数对称轴上是否存在点P,使
 的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.(3)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合). 过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当
 面积S最大时,求m的值.
面积S最大时,求m的值.
相关试题

