【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= ![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是 . (把你认为正确结论的序号都填上)
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是 . (把你认为正确结论的序号都填上) 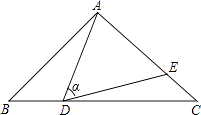
参考答案:
【答案】①②④
【解析】解:作AH⊥BC于H,如图, 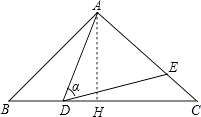
∵AB=AC,
∴∠B=∠C=α,BH=CH,
而∠ADE=∠B=α,
∴∠ADE=∠C,
而∠DAE=∠CAD,
∴△ADE∽△ACD,所以①正确;
在Rt△ABH中,cosB= ![]() ,
,
∴BH=10× ![]() =8,
=8,
∴BC=2BH=16,
当BD=6,则CD=10,
∵∠ADC=∠B+∠BAD,
而∠ADE=∠B=α,
∴∠EDC=∠BAD,
在△ABD与△DCE中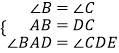 ,
,
∴△ABD≌△DCE,所以②正确;
∵∠B=∠C,∠BAD=∠CDE,
∴△ABD∽△DCE,
△DCE为直角三角形,当∠DEC=90°,则∠ADB=90°,BD为8;当∠EDC=90°,则∠BAD=90°,BD= ![]() =
= ![]() ,所以③错误;
,所以③错误;
设BD=x,则CD=16﹣x,
由△ABD∽△DCE得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴CE=﹣ ![]() (x﹣8)2+6.4,
(x﹣8)2+6.4,
∴CE的最大值为6.4,
∴0<CE≤6.4,所以④正确.
所以答案是①②④.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
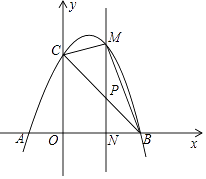
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P(3a,a)是反比例函数y=
 (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y=
B.y=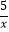
C.y=
D.y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,斜边AB=5厘米,BC=a厘米,AC=b厘米,a>b,且a、b是方程x2﹣(m﹣1)x+m+4=0的两根,Rt△ABC的面积为平方厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
 +(
+(  )﹣1﹣2cos60°+(2﹣π)0 .
)﹣1﹣2cos60°+(2﹣π)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6.将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.
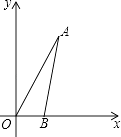
(1)请在图中画出△COD;
(2)求点A旋转过程中所经过的路程(精确到0.1). -
科目: 来源: 题型:
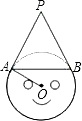
查看答案和解析>>【题目】如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠APB的度数.
相关试题

