【题目】如图所示,点P(3a,a)是反比例函数y= ![]() (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y= ![]()
B.y= ![]()
C.y= ![]()
D.y= ![]()
参考答案:
【答案】D
【解析】解:由于函数图像关于原点对称,所以阴影部分面积为 ![]() 圆面积,
圆面积,
则圆的面积为10π×4=40π.
因为P(3a,a)在第一象限,则a>0,3a>0,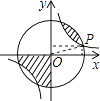
根据勾股定理,OP= ![]() =
= ![]() a.
a.
于是π ![]() =40π,a=±2,(负值舍去),故a=2.
=40π,a=±2,(负值舍去),故a=2.
P点坐标为(6,2).
将P(6,2)代入y= ![]() ,
,
得:k=6×2=12.
反比例函数解析式为:y= ![]() .
.
故选:D.
【考点精析】认真审题,首先需要了解反比例函数的图象(反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点),还要掌握反比例函数的性质(性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE=
 ,CQ=5,求AF的值.
,CQ=5,求AF的值.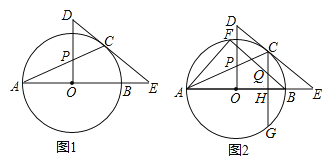
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠AGE,∠D=∠1,且∠1+∠2=180°,则下列结论:①CE∥BF,②∠A=∠D,③AB∥CD,④∠C=∠B,其中正确的结论有( )
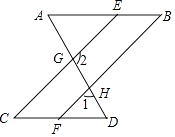
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列证明:
如图,已知DE⊥AC于点E,BC⊥AC于点C,FG⊥AB于点G,∠1=∠2,求证:CD⊥AB.
证明:∵DE⊥AC,BC⊥AC(已知),
∴DE∥(),
∴∠2=(两直线平行,内错角相等),
∵∠1=∠2,(已知),
∴∠1=(),
∴GF∥CD(),
∵FG⊥AB(已知),
∴CD⊥AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值: (
 a2bab2)(1
a2bab2)(1 ab2a2b) ,其中 a=3, b=2 .
ab2a2b) ,其中 a=3, b=2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把点P(-1,-2)向上平移4个单位长度所得点的坐标是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学科内综合题:现把10个数:﹣1,23,15,12,0,﹣31,﹣11,29,43,﹣62.分别写在10张纸条上,然后把纸条放进外形,颜色完全相同的小球内,再把这10个小球放进一个大玻璃瓶中,从中任意取一球,得到正数的可能性与得到负数的可能性哪个大.
相关试题

