【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.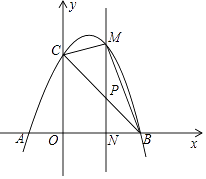
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
参考答案:
【答案】
(1)
解:在y=﹣x2+2x+3中,令x=0可得y=3,
∴C(0,3),
令y=0,可得﹣x2+2x+3=0,解得x=3或x=﹣1,
∴A(﹣1,0),B(3,0)
(2)
解:设直线BC的解析式为y=kx+b,则有 ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为y=﹣x+3.
设P(t,﹣t+3),则M(t,﹣t2+2t+3),
∴PM=(﹣t2+2t+3)﹣(﹣t+3)=﹣t2+3t.
∴S△BCM= ![]() PM(ON+BN)=
PM(ON+BN)= ![]() PMOB=
PMOB= ![]() ×3(﹣t2+3t)=﹣
×3(﹣t2+3t)=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当t= ![]() 时,△BCM的面积最大,此时P点坐标为(
时,△BCM的面积最大,此时P点坐标为( ![]() ,
, ![]() )
)
(3)
解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的对称轴为直线x=1,
∴设Q(1,m),且C(0,3),N( ![]() ,0),
,0),
∴CN= ![]() =
= ![]() ,CQ=
,CQ= ![]() =
= ![]() ,NQ=
,NQ= ![]() =
= ![]() ,
,
∵△CNQ为直角三角形,
∴分点C为直角顶点、点Q为直角顶点和点N为直角顶点三种情况:
①当点C为直角顶点时,则有CN2+CQ2=NQ2,
即( ![]() )2+(m2﹣6m+10)=
)2+(m2﹣6m+10)= ![]() +m2,解得m=
+m2,解得m= ![]() ,
,
此时Q点坐标为(1, ![]() );
);
②当点Q为直角顶点时,则有NQ2+CQ2=CN2,
即(m2﹣6m+10)+ ![]() +m2=(
+m2=( ![]() )2,解得x=
)2,解得x= ![]() 或x=
或x= ![]() ,
,
此时Q点坐标为(1, ![]() )或(1,
)或(1, ![]() );
);
③当点N为直角顶点时,则有NQ2+CN2=CQ2,
即( ![]() )2+
)2+ ![]() +m2=m2﹣6m+10,解得m=﹣
+m2=m2﹣6m+10,解得m=﹣ ![]() ,
,
此时Q点坐标为(1,﹣ ![]() );
);
综上可知Q点的坐标为(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,﹣
)或(1,﹣ ![]() )
)
【解析】(1)在抛物线解析式中,令x=0可求得C点坐标,令y=0则可求得A、B的坐标;(2)由B、C的坐标可求得直线BC的解析式为y=﹣x+3,可设P点坐标为(t,﹣t+3),则可表示出M点坐标,则可求得PM的长,从而可用t表示出△BCM的面积,再利用二次函数的性质可求得当△BCM的面积最大时t的值,可求得P点坐标;(3)由(2)可知N点坐标,设Q点坐标为(1,m),则可用m分别表示出QN、QC及CN,分点C为直角顶点、点Q为直角顶点和点N为直角顶点三种情况,分别根据勾股定理可得到关于m的方程,可求得m的值,可求得Q点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年以来,国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策,各地政府高度重视、积极响应,中国掀起了大众创业万众创新的新浪潮.某创新公司生产营销A、B两种新产品,根据市场调研,发现如下信息: 信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系y=ax2+bx,当x=1时,y=7;当x=2时,y=12.
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系y=2x.
根据以上信息,解答下列问题:
(1)求a,b的值;
(2)该公司准备生产营销A、B两种产品共10吨,请设计一个生产方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,∠B=60°,D为AB的中点,∠EDF=90°,DE交AC于点G,DF经过点C.
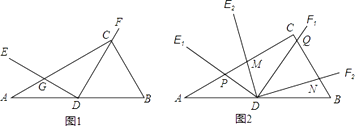
(1)求∠ADE的度数;
(2)如图2,将图1中的∠EDF绕点D顺时针方向旋转角α(0°<α<60°),旋转过程中的任意两个位置分别记为∠E1DF1 , ∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求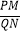 的值;
的值;
(3)若图1中∠B=β(60°<β<90°),(2)中的其余条件不变,判断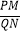 的值是否为定值?如果是,请直接写出这个值(用含β的式子表示);如果不是,请说明理由.
的值是否为定值?如果是,请直接写出这个值(用含β的式子表示);如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣7﹣5.
(2)(﹣15)﹣(﹣9)
(3)(﹣5)×(﹣7)+20÷(﹣4)
(4)(
 )×(﹣36)
)×(﹣36)(5)﹣81÷
 ×
× ÷(﹣16)
÷(﹣16)(6)5
 ﹣(﹣2
﹣(﹣2 )+(﹣3
)+(﹣3 )﹣(+4
)﹣(+4 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P(3a,a)是反比例函数y=
 (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y=
B.y=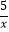
C.y=
D.y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,斜边AB=5厘米,BC=a厘米,AC=b厘米,a>b,且a、b是方程x2﹣(m﹣1)x+m+4=0的两根,Rt△ABC的面积为平方厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=
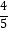 .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是 . (把你认为正确结论的序号都填上)
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是 . (把你认为正确结论的序号都填上) 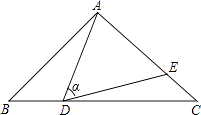
相关试题

