【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 与
与![]() 关于
关于![]() 轴对称,交
轴对称,交![]() 轴于点
轴于点![]() ,
,
(1)求直线![]() 的解析式;
的解析式;
(2)过点![]() 在
在![]() 外作直线
外作直线![]() ,过
,过![]() 点作
点作![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 于点
于点 ![]() .求证:
.求证:![]()
(3)如图2,如果![]() 沿
沿![]() 轴向右平移,
轴向右平移,![]() 边交
边交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 的延长线上的一点,且
的延长线上的一点,且![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,在
,在![]() 平移的过程中,
平移的过程中,![]() 的长度是否为定值,请说明理由.
的长度是否为定值,请说明理由.

参考答案:
【答案】(1)![]() ;(2)见解析;(3)是,理由见解析
;(2)见解析;(3)是,理由见解析
【解析】
(1)先根据对称点的特点得出C点的坐标,然后利用待定系数法即可求出直线BC的解析式;
(2)首先通过等腰直角三角形的性质得出![]() ,然后证明
,然后证明![]() ,则有
,则有![]() ,最后利用
,最后利用![]() 即可证明;
即可证明;
(3)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,首先根据平行线的性质和等腰三角形的性质得出
,首先根据平行线的性质和等腰三角形的性质得出![]() ,进而可证
,进而可证![]() ,则有
,则有![]() ,最后利用
,最后利用![]() 则可证明OP为定值.
则可证明OP为定值.
解:(1)![]() ,直线
,直线![]() 与
与![]() 关于
关于![]() 轴对称,交
轴对称,交![]() 轴于点
轴于点![]() ,
,
∴点![]() 坐标是
坐标是![]() .
.
设直线![]() 解析式为
解析式为![]() ,
,
把![]() 代入得:
代入得:
![]() 解得:
解得:![]()
∴直线BC的解析式为![]() ;
;
(2)![]() ,
,
![]() ,
,![]() 和
和![]() 是全等的等腰直角三角形,
是全等的等腰直角三角形,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
在![]() 中
中
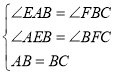
![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() 为定值,理由如下:
为定值,理由如下:
过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,
,
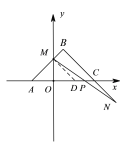
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为定值.
为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”是我国的传统佳节,历来有吃“粽子”的习俗.我市某食品加工厂,拥有A、B两条粽子加工生产线.原计划A生产线每小时加工粽子个数是B生产线每小时加工粽子个数的
 .
.(1)若A生产线加工4000个粽子所用时间与B生产线加工4000个粽子所用时间之和恰好为18小时,则原计划A、B生产线每小时加工粽子各是多少个?
(2)在(1)的条件下,原计划A、B生产线每天均加工a小时,由于受其他原因影响,在实际加工过程中,A生产线每小时比原计划少加工100个,B生产线每小时比原计划少加工50个.为了尽快将粽子投放到市场,A生产线每天比原计划多加工3小时,B生产线每天比原计划多加工
 a小时.这样每天加工的粽子不少于6300个,求a的最小值.
a小时.这样每天加工的粽子不少于6300个,求a的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)甲,乙,丙三位学生进入了“校园朗诵比赛”冠军、亚军和季军的决赛,他们将通过抽签来决定比赛的出场顺序.
(1)求甲第一个出场的概率;
(2)求甲比乙先出场的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于
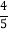 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=kx+1与y=﹣
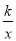 (k≠0)的图象大致是( )
(k≠0)的图象大致是( )A.
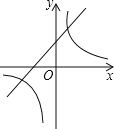 B.
B.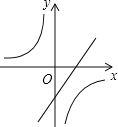
C.
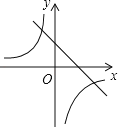 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
相关试题

