【题目】(8分)在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
参考答案:
【答案】(1)公平;(2)不公平.
【解析】试题分析:(1)、依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率,比较即可.(2)、解题思路同上.
试题解析:(1)、甲同学的方案不公平.理由如下:
列表法,
小明 | 2 | 3 | 4 | 5 |
2 | (2,3) | (2,4) | (2,5) | |
3 | (3,2) | (3,4) | (3,5) | |
4 | (4,2) | (4,3) | (4,5) | |
5 | (5,2) | (5,3) | (5,4) |
所有可能出现的结果共有12种,其中抽出的牌面上的数字之和为奇数的有:8种,故小明获胜的概率为:![]() =
=![]() ,则小刚获胜的概率为:
,则小刚获胜的概率为:![]() , 故此游戏两人获胜的概率不相同,即他们的游戏规则不公平;
, 故此游戏两人获胜的概率不相同,即他们的游戏规则不公平;
(2)、不公平.理由如下:
小明 | 3 | 4 | |
2 | (2,3) | (2,4) | |
3 | (3,2) | (3,4) | |
4 | (4,2) | (4,3) |
所有可能出现的结果共有6种,其中抽出的牌面上的数字之和为奇数的有:4种,故小明获胜的概率为:![]() =
=![]() ,则小刚获胜的概率为:
,则小刚获胜的概率为:![]() , 故此游戏两人获胜的概率不相同,即他们的游戏规则不公平.
, 故此游戏两人获胜的概率不相同,即他们的游戏规则不公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线
 与
与 轴交于点
轴交于点 ,交
,交 轴于点
轴于点 ,直线
,直线 与
与 关于
关于 轴对称,交
轴对称,交 轴于点
轴于点 ,
,(1)求直线
 的解析式;
的解析式;(2)过点
 在
在 外作直线
外作直线 ,过
,过 点作
点作 于点
于点 ,过
,过 点作
点作 于点
于点  .求证:
.求证:
(3)如图2,如果
 沿
沿 轴向右平移,
轴向右平移, 边交
边交 轴于点
轴于点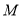 ,点
,点 是
是 的延长线上的一点,且
的延长线上的一点,且 ,
, 与
与 轴交于点
轴交于点 ,在
,在 平移的过程中,
平移的过程中, 的长度是否为定值,请说明理由.
的长度是否为定值,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于
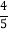 ,求m的值.
,求m的值. -
科目: 来源: 题型:
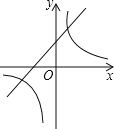
查看答案和解析>>【题目】在同一直角坐标系中,函数y=kx+1与y=﹣
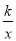 (k≠0)的图象大致是( )
(k≠0)的图象大致是( )A.
 B.
B.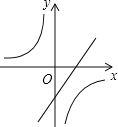
C.
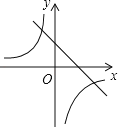 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )

A. 130°B. 120°C. 110°D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
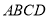 的边
的边 轴,垂足为点
轴,垂足为点 ,顶点
,顶点 在第二象限,顶点
在第二象限,顶点 在
在 轴的正半轴上,反比例函数
轴的正半轴上,反比例函数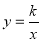 (
( ,
, )的图像同时经过顶点
)的图像同时经过顶点 、
、 ,若点
,若点 的横坐标为1,
的横坐标为1,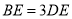 .则
.则 的值为( )
的值为( )
A.
 B.3C.
B.3C. D.5
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由.
(2)求∠DBE的度数.
(3)若把AD左右平行移动,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出此时∠ADB的度数;若不存在,请说明理由.

相关试题

