【题目】已知在平面直角坐标系中,三角形ABC的位置如图所示.
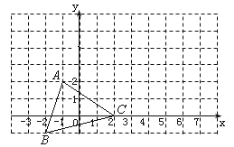
(1)请写出A、B、C三点的坐标;
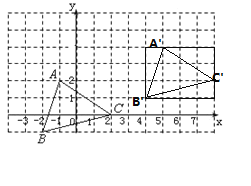
(2)将三角形ABC向右平移6个单位, 再向上平移2个单位,请在图中作出平移后的三角形A'B'C',并写出三角形A'B'C'各点的坐标;
(3)求出三角形A'B'C'的面积.
参考答案:
【答案】(1)A(-1,2),B(-2,-1),A(2,0);(2)图见解析,A'(5,4),B'(4,1),C'(8,2);(3)5.5
【解析】
(1)根据直角坐标系直接写出;
(2)先把各顶点进行平移,再依次连接得到三角形A'B'C',再根据直角坐标系写出坐标;
(3)根据割补法即可求出面积.
(1)A(-1,2),B(-2,-1),A(2,0);
(2)如图,三角形A'B'C'为所求,A'(5,4),B'(4,1),C'(8,2);
(3)三角形A'B'C'的面积为4×3-![]() ×4×1-
×4×1-![]() ×1×3-
×1×3-![]() ×3×2=5.5.
×3×2=5.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】疫情期间,某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价x(元)与日销售量y(只)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(只)
2000
1500
1200
1000
(1)猜测并确定y与x之间的函数关系式;
(2)设经营此口罩的销售利润为W元,求出W与x之间的函数关系式?
(3)若物价局规定此口罩的售价最高不能超过10元/只,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1500名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称
人数
乒乓球
42
羽毛球
a
排球
15
篮球
33
足球
b
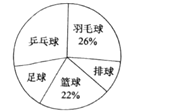

解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,a=________,b=________;
(3)试估计上述1500名学生中最喜欢乒乓球运动的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB,A(2,1),B(4,3),现将线段AB沿y轴方向向下平移得到线段MN,直线y=mx+b过M、N两点,且M、N两点恰好也落在双曲线y=
 的一条分支上,
的一条分支上,
(1)求反比例函数和一次函数的解析式.
(2)直接写出不等式mx+b-
 ≥0的解集
≥0的解集(3)若点C(x1,a),D(x2,a-1)在双曲线y=
 上,试比较x1和x2的大小.
上,试比较x1和x2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB,AC与⊙O相切于点B,C,∠A=50°,点P是圆上异于B,C的一动点,则∠BPC的度数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

相关试题

