【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.
(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
参考答案:
【答案】
(1)50
(2)解:如图:

(3)解:根据题意如表:

∵共有12种等可能的结果数,其中一名男生和一名女生的共有7种,
∴P= ![]() ,
,
答:选中一名男生和一名女生的概率为: ![]() .
.
【解析】解:(1)因为合格的男生有2人,女生有1人,共计2+1=3人,
又因为评级合格的学生占6%,
所以全班共有:3÷6%=50(人).
故答案为:50.(2)根据题意得:
女生评级3A的学生是:50×16%﹣3=8﹣3=5(人),
女生评级4A的学生是:50×50%﹣10=25﹣10=15(人),
(2)如图:

(3)根据题意如表:

∵共有12种等可能的结果数,其中一名男生和一名女生的共有7种,
∴P= ![]() ,
,
答:选中一名男生和一名女生的概率为: ![]() .
.
故答案为:(1)50;(2)见解答过程;(3)![]() .
.
(1)先求得合格的总人数为3,然后依据总数=频数÷百分比求解即可;
(2)先求得评级为3A和4A的人数,从而可求得求得评级为3A和4A的女上人数;
(3)先依据列出表格,然后再求得所有可能出现的情况以及恰好一男一女的情况数,最后,利用概率公式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知x=
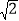 -1,求x2+3x-1的值.(2)已知a=1-
-1,求x2+3x-1的值.(2)已知a=1-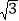 ,b=1+
,b=1+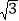 ,求2a2+2b2-3ab-a+b的值.
,求2a2+2b2-3ab-a+b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 把解集在数轴上表示,并求不等式组的整数解.
把解集在数轴上表示,并求不等式组的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,回答有关问题:在实数这章中,遇到过
 ,
, ,
, ,
, ,
, 这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开得尽方,可以利用
这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开得尽方,可以利用 =
= (a≥0,b≥0);
(a≥0,b≥0); (a≥0,b>0)将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时,这样的二次根式叫做最简二次根式,例如,
(a≥0,b>0)将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时,这样的二次根式叫做最简二次根式,例如,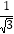 化成最简二次根式是
化成最简二次根式是 ,
, 化成最简二次根式是3
化成最简二次根式是3 ,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子中的
,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子中的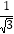 和
和 就是同类二次根式.
就是同类二次根式.(1)请判断下列各式中,哪些是同类二次根式?
 ,
, ,
, ,
, ,
,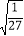 ,
, .
.(2)二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算:
 +
+ -
- -
- +
+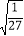 -
- .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,解答下面的问题:
我们知道方程
 有无数个解,但在实际生活中我们往往只需求出其
有无数个解,但在实际生活中我们往往只需求出其正整数解.
例:由
 ,得:
,得: ,(x、y为正整数)
,(x、y为正整数)∴
 ,则有
,则有 .又
.又 为正整数,则
为正整数,则 为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入
为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入 ∴2x+3y=12的正整数解为
∴2x+3y=12的正整数解为
问题:
(1)请你写出方程
 的一组正整数解: .
的一组正整数解: .(2)若
 为自然数,则满足条件的x值为 .
为自然数,则满足条件的x值为 .(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在进行二次根式化简时,我们有时会碰上如
 ,
, ,
, 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: =
=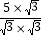 =
= ,
, =
= =
= ,
, =
= =
= =
= -1,
-1, 还可以用以下方法化简:
还可以用以下方法化简: =
= =
= =
= =
= -1.以上这种化简的方法叫做分母有理化.(1)请化简
-1.以上这种化简的方法叫做分母有理化.(1)请化简 =________;(2)若a是
=________;(2)若a是 的小数部分则
的小数部分则 =________;(3)矩形的面积为3
=________;(3)矩形的面积为3 +1,一边长为
+1,一边长为 -2,则它的周长为________;(4)化简
-2,则它的周长为________;(4)化简 +
+ +
+ +…+
+…+ .
.
相关试题

