【题目】已知△ABC,D、E分别为AC、AB中点,BD和CE交于点O,BD和CE是一元二次方程x2﹣kx+24=0的两个不等实根,则△BOE面积的最大值为( )
A.![]()
B.2
C.![]()
D.4
参考答案:
【答案】C
【解析】解:∵D、E分别为AC、AB中点,BD和CE交于点O,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
∴△DOE∽△BOC,
∴OD:OB=OE:OC=DE:BC=1:2,
∴OE= ![]() CE,OB=
CE,OB= ![]() BD,
BD,
∵BD和CE是一元二次方程x2﹣kx+24=0的两个不等实根,
∴BDCE=24,
若△BOE面积最大,则△BOE是直角三角形,
分两种情况:
①若∠BEO=90°,则CE⊥AB,
∵E是AB的中点,
∴AC=BC,
同理:AB=BC,
则△ABC是等边三角形,
∴BD=CE,不合题意;
②当∠BOE=90°时,△BOE的面积= ![]() OEOB=
OEOB= ![]() ×
× ![]() CE×
CE× ![]() BD=
BD= ![]() ×
× ![]() ×
× ![]() ×24=
×24= ![]() ;
;
故选:C.
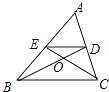
【考点精析】根据题目的已知条件,利用根与系数的关系和三角形中位线定理的相关知识可以得到问题的答案,需要掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,BC的垂直平分线交BC于E,交AC于D,且AD=DE
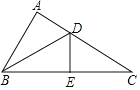
(1)求证:∠ABD=∠C;
(2)求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣2.8+(﹣3.6)+(+3)﹣(﹣3.6)
(2)(﹣4)2010×(﹣0.25)2009+(﹣12)×(
 ﹣
﹣ +
+ )
)(3)13°16'×5﹣19°12'÷6
-
科目: 来源: 题型:
查看答案和解析>>【题目】若α、β为方程2x2﹣5x﹣1=0的两个实数根,则2α2+3αβ+5β的值为( )
A.﹣13
B.12
C.14
D.15 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
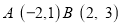 ,直线
,直线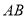 交
交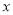 轴于点
轴于点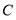 ,平移线段
,平移线段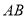 至
至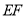 ,若点
,若点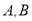 的对应点分别为
的对应点分别为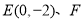 ,则线段
,则线段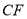 的长为______.
的长为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,二次函数y=ax2+bx+c(b>0)与一次函数y=ax+c的大致图象可能是( )
A.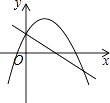
B.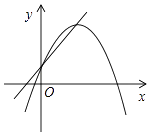
C.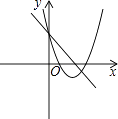
D.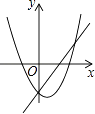
相关试题

