【题目】已知:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 方向向终点
方向向终点![]() 运动;同时,动点
运动;同时,动点![]() 也从点
也从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 方向向终点
方向向终点![]() 运动.设两点运动的时间为
运动.设两点运动的时间为![]() 秒
秒![]() .
.
![]() 连接
连接![]() ,在点
,在点![]() 、
、![]() 运动过程中,
运动过程中,![]() 与
与![]() 是否始终相似?请说明理由;
是否始终相似?请说明理由;
![]() 连接
连接![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 连接
连接![]() 、
、![]() ,是否存在
,是否存在![]() 的值,使
的值,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
![]() 探索:把
探索:把![]() 沿直线
沿直线![]() 折叠成
折叠成![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 是直角三角形时,请直接写出
是直角三角形时,请直接写出![]() 的值.
的值.

参考答案:
【答案】![]() 相似,理由见解析;
相似,理由见解析;![]() ∴
∴![]() ;
;![]() 存在,
存在,![]() 的值为
的值为![]() ;
;![]() ,
,![]() .
.
【解析】
(1)已知AC、BC的长,根据勾股定理即可求得AB的长,根据![]() ,进而即可求得△APQ∽△ABC.
,进而即可求得△APQ∽△ABC.
(2)根据△APQ∽△ABC即可求得![]() ,即可求得S关于t的方程式.
,即可求得S关于t的方程式.
(3)先求证△PCQ∽△QBC进而可以得![]() ,即
,即![]() ,求得t的值即可解题.
,求得t的值即可解题.
(4)分别用t表示PE、EQ、BQ的值,根据勾股定理即可求得t的值,即可解题.
(1)相似
∵∠ACB=〖90〗^
∴AB=√(AC^2+BC^2 )=5
∵PA=5/4 t,AQ=t
∴PA/AB=AQ/BC=t/4
∵∠A=∠A
∴△APQ∽△ABC
(2)∵△APQ∽△ABC
∴∠PQA=∠C=〖90〗^
∵PQ/BC=AQ/AC
∴PQ/3=t/4
∴PQ=3/4 t
∵CQ=4-t
∴S=1/23/4 t(4-t)=-3/8 t^2+3/2 t
(3)存在
∵PC⊥BQ
∴∠PCQ+∠BQC=〖90〗^
∵∠CBQ+∠BQC=〖90〗^
∴∠PCQ=∠CBQ
∵∠PQC=∠BCQ=〖90〗^
∴△PCQ∽△QBC
∴PQ/CQ=CQ/BC
∴(3/4 t)/(4-t)=(4-t)/3
∴t_1=(41+3√73)/8(舍去)t_2=(41-3√73)/8
∴存在t的值为(41-3√73)/8,使PC⊥BQ.
(4)t_1=1,t_2=7/4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC,若CE=5,则BC等于( )
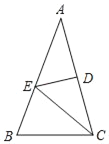
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】4张相同的卡片上分别写有数字2,3,4,5将卡片的背面向上,洗匀后从中任意抽取1 张,将卡片上的数字作为被减数;一只不透明的袋子中装有标号2,3,4的3个小球,这些球除标号外都相同,搅匀后从中任意摸出一个球,将摸到的球的标号作为减数.
(1)用树状图或列表的方法求这两个数的差为0的概率;
(2)如果游戏规则规定:当抽到的这两个数的差为非负数时,则甲获胜;否则,乙获胜,你认为这样的规则公平吗?如果不公平,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD 中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=
 ,则∠ACB的度数为( )
,则∠ACB的度数为( )
A.
 α B. 90°-
α B. 90°- α C. 45° D. α-45°
α C. 45° D. α-45° -
科目: 来源: 题型:
查看答案和解析>>【题目】某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.平均修建每公顷大棚要用的支架、塑料膜等材料的费用为
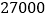 元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为
元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为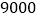 .每公顷大棚的年平均经济收益为
.每公顷大棚的年平均经济收益为 元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为
元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为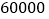 元.
元. 一年中这个村修建了多少公顷蔬菜大棚?
一年中这个村修建了多少公顷蔬菜大棚? 若要使收益达到最大,请问应修建多少公顷大棚?并说明理由.
若要使收益达到最大,请问应修建多少公顷大棚?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
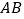 是
是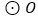 的直径,
的直径,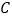 是
是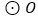 上一点,
上一点,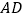 和过点
和过点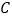 的切线互相垂直,垂足为点
的切线互相垂直,垂足为点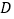 .
.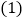 如图
如图 ,求证:
,求证: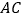 平分
平分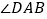 ;
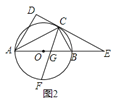
; 如图
如图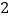 ,直线
,直线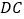 与
与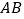 的延长线交于点
的延长线交于点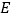 ,
, 的平分线交
的平分线交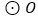 于点
于点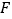 ,
,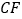 交
交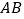 于点
于点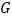 ,求证:
,求证: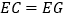 ;
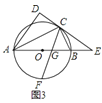
;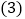 在
在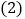 的条件下,如图
的条件下,如图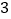 ,若
,若 ,
,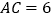 ,求
,求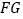 的长.
的长.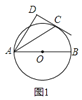
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在
 中,
中,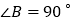 ,
,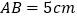 ,
,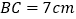 ,点
,点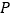 从点
从点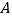 开始沿
开始沿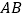 边向点
边向点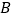 以
以 的速度移动,点
的速度移动,点 从点
从点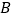 开始沿
开始沿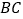 边向点
边向点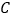 以
以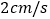 的速度移动.
的速度移动.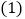 如果
如果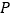 ,
, 分别从
分别从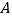 ,
,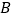 同时出发,那么几秒后,
同时出发,那么几秒后,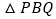 的面积等于
的面积等于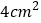 ?
?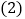 如果
如果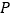 ,
, 分别从
分别从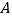 ,
,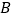 同时出发,那么几秒后,
同时出发,那么几秒后,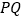 的长度等于
的长度等于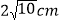 ?
?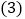 在
在 中,
中, 的面积能否等于
的面积能否等于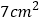 ?说明理由.
?说明理由.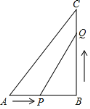
相关试题

