【题目】已知,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为点
的切线互相垂直,垂足为点![]() .
.
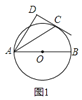
![]() 如图
如图![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
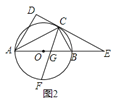
![]() 如图
如图![]() ,直线
,直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
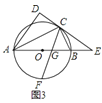
![]() 在
在![]() 的条件下,如图
的条件下,如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】![]() 证明见解析;(2)证明见解析;(3)
证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接OC,根据切线与圆的关系和直角三角形内角之间的关系,可以推出AC平分∠DAB;
(2)根据圆周角定理以及三角形的外角的性质定理证明∠ECG=∠EGC,根据等角对等边即可证得;
(3)证明△ECB∽△EAC,根据相似三角形的性质求得![]() ,在直角△EOC中利用勾股定理列方程求得BE和CE,进而求得BG,然后根据△AGF∽△CGB,根据相似三角形的性质求得FG的长.
,在直角△EOC中利用勾股定理列方程求得BE和CE,进而求得BG,然后根据△AGF∽△CGB,根据相似三角形的性质求得FG的长.
![]() 证明:连接
证明:连接![]() ,如图
,如图![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
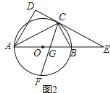
即![]() 平分
平分![]() ;
;
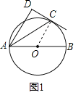
![]() 证明:如图
证明:如图![]() ,∵
,∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 解:如图
解:如图![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.

∵![]() 是直径,
是直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 是直径,
是直径,
∴![]() .
.
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() ,在
,在![]() 中,
中,![]() ,
,
解得![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD 中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=
 ,则∠ACB的度数为( )
,则∠ACB的度数为( )
A.
 α B. 90°-
α B. 90°- α C. 45° D. α-45°
α C. 45° D. α-45° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
 中,
中, ,
, ,
, ,动点
,动点 从点
从点 出发,以每秒
出发,以每秒 个单位的速度沿
个单位的速度沿 方向向终点
方向向终点 运动;同时,动点
运动;同时,动点 也从点
也从点 出发,以每秒
出发,以每秒 个单位的速度沿
个单位的速度沿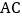 方向向终点
方向向终点 运动.设两点运动的时间为
运动.设两点运动的时间为 秒
秒 .
. 连接
连接 ,在点
,在点 、
、 运动过程中,
运动过程中, 与
与 是否始终相似?请说明理由;
是否始终相似?请说明理由; 连接
连接 ,设
,设 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式;
的函数关系式; 连接
连接 、
、 ,是否存在
,是否存在 的值,使
的值,使 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由; 探索:把
探索:把 沿直线
沿直线 折叠成
折叠成 ,设
,设 与
与 交于点
交于点 ,当
,当 是直角三角形时,请直接写出
是直角三角形时,请直接写出 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.平均修建每公顷大棚要用的支架、塑料膜等材料的费用为
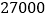 元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为
元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为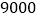 .每公顷大棚的年平均经济收益为
.每公顷大棚的年平均经济收益为 元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为
元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为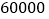 元.
元. 一年中这个村修建了多少公顷蔬菜大棚?
一年中这个村修建了多少公顷蔬菜大棚? 若要使收益达到最大,请问应修建多少公顷大棚?并说明理由.
若要使收益达到最大,请问应修建多少公顷大棚?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在
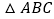 中,
中,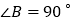 ,
,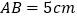 ,
,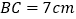 ,点
,点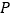 从点
从点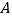 开始沿
开始沿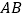 边向点
边向点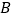 以
以 的速度移动,点
的速度移动,点 从点
从点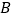 开始沿
开始沿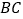 边向点
边向点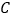 以
以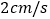 的速度移动.
的速度移动.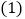 如果
如果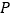 ,
, 分别从
分别从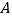 ,
,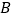 同时出发,那么几秒后,
同时出发,那么几秒后,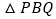 的面积等于
的面积等于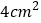 ?
?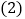 如果
如果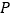 ,
, 分别从
分别从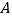 ,
,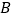 同时出发,那么几秒后,
同时出发,那么几秒后,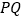 的长度等于
的长度等于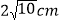 ?
?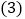 在
在 中,
中, 的面积能否等于
的面积能否等于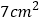 ?说明理由.
?说明理由.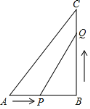
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
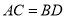 ,
, ,
, 与
与 交于点
交于点 .有下列结论:
.有下列结论:
①
 ;
;②
 ;
;③ 点
 在线段
在线段 的垂直平分线上;
的垂直平分线上;④
 、
、 分别平分
分别平分 和
和 ;
;以上结论正确的个数有( )
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】符合下列条件之一的四边形不一定是菱形的是( )
A. 四条边相等
B. 两组邻边分别相等
C. 对角线相互垂直平分
D. 两条对角线分别平分一组对角
相关试题

