【题目】分别判别数3、﹣4、5是不是下列一元二次方程的根.
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() .
.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析;(4)见解析.
【解析】
分别将3、﹣4、5代入下列方程进行验证即可.
解:(1)将x=3代入![]() 可得:15=15,故x=3是该一元二次方程的根,
可得:15=15,故x=3是该一元二次方程的根,
将x=-4代入![]() 可得:8=8,故x=-4是该一元二次方程的根,
可得:8=8,故x=-4是该一元二次方程的根,
将x=5代入![]() 可得:35≠17,故x=5不是该一元二次方程的根;
可得:35≠17,故x=5不是该一元二次方程的根;
(2)将x=3代入![]() 可得:-11≠3,故x=3不是该一元二次方程的根,
可得:-11≠3,故x=3不是该一元二次方程的根,
将x=-4代入![]() 可得:-4=-4,故x=-4是该一元二次方程的根,
可得:-4=-4,故x=-4是该一元二次方程的根,
将x=5代入![]() 可得:5=5,故x=5是该一元二次方程的根;
可得:5=5,故x=5是该一元二次方程的根;
(3)将x=3代入![]() 可得:15=15,故x=3是该一元二次方程的根,
可得:15=15,故x=3是该一元二次方程的根,
将x=-4代入![]() 可得:-55≠8,故x=-4不是该一元二次方程的根,
可得:-55≠8,故x=-4不是该一元二次方程的根,
将x=5代入![]() 可得:35=35,故x=5是该一元二次方程的根;
可得:35=35,故x=5是该一元二次方程的根;
(4)将x=3代入![]() 可得:0≠6,故x=3不是该一元二次方程的根,
可得:0≠6,故x=3不是该一元二次方程的根,
将x=-4代入![]() 可得:42≠6,故x=-4不是该一元二次方程的根,
可得:42≠6,故x=-4不是该一元二次方程的根,
将x=5代入![]() 可得:6≠6,故x=5是该一元二次方程的根.
可得:6≠6,故x=5是该一元二次方程的根.
-
科目: 来源: 题型:
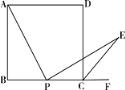
查看答案和解析>>【题目】如图,在正方形ABCD中,P是BC上一动点,(不与B、C重合)① CE平分∠DCF,② AP⊥PE,③ AP=EP.以此三个条件中的两个为条件,另一个为结论,可构成三个命题,即:①② ③,①③ ②,②③ ①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请选择一个你认为正确的命题给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机械厂甲、乙两个生产车间承担生产同一种零件的任务,甲、乙两车间共有50人,甲车间平均每人每天生产零件30个.乙车间平均每人每天生产零件20个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为1300个.
(1)求甲、乙两车间各有多少人?
(2)该机械厂改进了生产技术。在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间.调整后甲、乙两车间平均每人每天生产零件都比原来多5个,甲乙两车间每天生产零件总数之和是1480个,且甲、乙两车间每人的计件工资(按完成件数发放工资)分别是12元和9元,求甲、乙两车间每天计件收入总和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠ACB=90°,AC:BC=4:3,O是BC上一点,⊙O交AB于点D,交BC延长线于点E.连接ED,交AC于点G,且AG=AD.
(1)求证:AB与⊙O相切;
(2)设⊙O与AC的延长线交于点F,连接EF,若EF∥AB,且EF=5,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列给出的条件中,能判定四边形
 为平行四边形的是( )
为平行四边形的是( )A.
 B.
B. 
C.
 D. ∠A=∠B,∠C=∠D
D. ∠A=∠B,∠C=∠D -
科目: 来源: 题型:
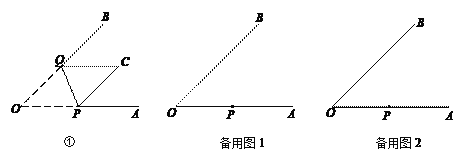
查看答案和解析>>【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2 cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处.
(1)①当PC∥QB时,OQ= cm;
②在OB上找一点Q,使PC⊥QB(尺规作图,保留作图痕迹);
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】光华中学库存若干套桌椅,准备修理后支援贫困山区学校.现有甲、乙两修理组,甲修理组单独完成任务需要12天,乙修理组单独完成任务需要24天.
(1)若由甲、乙两修理组同时修理,需多少天可以修好这些套桌椅?
(2)若甲、乙两修理组合作3天后,甲修理组因新任务离开,乙修理组继续工作.甲完 成新任务后,回库与乙又合作3天,恰好完成任务.问:甲修理组离开几天?
(3)学校需要每天支付甲修理组、乙修理组修理费分别为80元,120元.任务完成后, 两修理组收到的总费用为1920元,求甲修理组修理了几天?
相关试题

