【题目】某机械厂甲、乙两个生产车间承担生产同一种零件的任务,甲、乙两车间共有50人,甲车间平均每人每天生产零件30个.乙车间平均每人每天生产零件20个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为1300个.
(1)求甲、乙两车间各有多少人?
(2)该机械厂改进了生产技术。在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间.调整后甲、乙两车间平均每人每天生产零件都比原来多5个,甲乙两车间每天生产零件总数之和是1480个,且甲、乙两车间每人的计件工资(按完成件数发放工资)分别是12元和9元,求甲、乙两车间每天计件收入总和.
参考答案:
【答案】(1)甲车间有30人,乙车间有20人;(2)甲、乙两车间每天计件收入总和为15735元.
【解析】
(1)设甲车间有x人,乙车间有50-x人,根据甲、乙两车间共有50人和甲车间每天生产零件总数与乙车间每天生产零件总数之和为1300个列方程组成方程组解决问题;
(2)(2)设从甲车间调出a人到乙车间,表示出两个车间的人数,根据生产零件总数之和是1480个,列出方程求解.然后车间每天的收入=每人每天生产零件的个数×人数×每人的计件工资分别计算出甲乙两车间的收入求和即可.
(1)设甲车间有x人,乙车间有50-x人,由题意得,
![]()
解得x=30,50-x=20.
答:甲车间有30人,乙车间有20人;
(2)设从甲车间调出a人到乙车间,则甲车间有(30a)人,乙车间有(20+a)人,
35(30a)+25(20+a)=1480
解得:a=7
则甲车间每天生产:35(30a)=805件,乙车间每天生产:25(20+a)=675件.
所以收入总和为805×12+675×9=15735元
答:甲、乙两车间每天计件收入总和为15735元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是投影仪安装截面图.教室高EF=3.5 m,投影仪A发出的光线夹角∠BAC=30°,投影屏幕高BC=1.2 m.固定投影仪的吊臂AD=0.5 m,且AD⊥DE,AD∥EF,∠ACB=45°.求屏幕下边沿离地面的高度CF(结果精确到0.1 m).
(参考数据:tan15°≈0.27,tan30°≈0.58)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从甲地出发以每小时80 km的速度匀速驶往乙地,一段时间后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.货车行驶2.5 h后,在距乙地160 km处与轿车相遇.图中线段AB表示货车离乙地的距离y1 km与货车行驶时间x h的函数关系.
(1)求y1与x之间的函数表达式;
(2)若两车同时到达各自目的地,在同一坐标系中画出轿车离乙地的距离y2与x的图像,求该图像与x轴交点坐标并解释其实际意义.

-
科目: 来源: 题型:
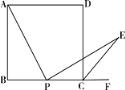
查看答案和解析>>【题目】如图,在正方形ABCD中,P是BC上一动点,(不与B、C重合)① CE平分∠DCF,② AP⊥PE,③ AP=EP.以此三个条件中的两个为条件,另一个为结论,可构成三个命题,即:①② ③,①③ ②,②③ ①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请选择一个你认为正确的命题给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠ACB=90°,AC:BC=4:3,O是BC上一点,⊙O交AB于点D,交BC延长线于点E.连接ED,交AC于点G,且AG=AD.
(1)求证:AB与⊙O相切;
(2)设⊙O与AC的延长线交于点F,连接EF,若EF∥AB,且EF=5,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】分别判别数3、﹣4、5是不是下列一元二次方程的根.
(1)
 ;
; (2)
 ;
; (3)
 ;
;(4)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列给出的条件中,能判定四边形
 为平行四边形的是( )
为平行四边形的是( )A.
 B.
B. 
C.
 D. ∠A=∠B,∠C=∠D
D. ∠A=∠B,∠C=∠D
相关试题

