【题目】已知,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,垂足为
,垂足为![]() .
.
(1)如图,连接![]() 、
、![]() .求证四边形
.求证四边形![]() 为菱形,并求
为菱形,并求![]() 的长;
的长;
(2)如图,动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,沿
两点同时出发,沿![]() 和
和![]() 各边匀速运动一周.即点
各边匀速运动一周.即点![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止,点
停止,点![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止.在运动过程中,
停止.在运动过程中,
①已知点![]() 的速度为每秒5
的速度为每秒5![]() ,点
,点![]() 的速度为每秒4
的速度为每秒4![]() ,运动时间为
,运动时间为![]() 秒,当
秒,当![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求![]() 的值.
的值.
②若点![]() 、
、![]() 的运动路程分别为
的运动路程分别为![]() 、
、![]() (单位:
(单位:![]() ,
,![]() ),已知
),已知![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形,写出
四点为顶点的四边形是平行四边形,写出![]() 与
与![]() 满足的数量关系式.(直接写出答案,不要求证明)
满足的数量关系式.(直接写出答案,不要求证明)

参考答案:
【答案】(1)证明略,![]() (2) ①
(2) ①![]() 秒. ②
秒. ②![]() 与
与![]() 满足的函数关系式是
满足的函数关系式是![]()
【解析】
试题(1)先证明四边形AFCE为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定;根据勾股定理即可求得AF的长;
(2)分情况讨论可知,当P点在BF上、Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可.
试题解析:(1)证明:①∵四边形![]() 是矩形
是矩形
∴![]() ∥
∥![]()
∴![]() ,
,![]()
∵![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]()
∴![]()
∴![]() ≌
≌![]()
∴![]()
∴四边形![]() 为平行四边形
为平行四边形
又∵![]()
∴四边形![]() 为菱形
为菱形
②设菱形的边长![]() ,则
,则![]()
在![]() 中,
中,![]()
解得![]()
∴![]()
(2)①显然当![]() 点在
点在![]() 上时,
上时,![]() 点在
点在![]() 上,此时
上,此时![]() 、
、![]() 、
、![]() 、
、![]() 四点不可能构成平行四边形;同理
四点不可能构成平行四边形;同理![]() 点在
点在![]() 上时,
上时,![]() 点在
点在![]() 或
或![]() 上,也不能构成平行四边形.因此只有当
上,也不能构成平行四边形.因此只有当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,才能构成平行四边形
上时,才能构成平行四边形
∴以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,![]()
∵点![]() 的速度为每秒10cm,点
的速度为每秒10cm,点![]() 的速度为每秒6cm,运动时间为
的速度为每秒6cm,运动时间为![]() 秒
秒
∴![]() ,
,
∴![]() ,解得
,解得![]()
∴以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,![]() 秒.
秒.
②由题意得,以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,点
四点为顶点的四边形是平行四边形时,点![]() 、
、![]() 在互相平行的对应边上.
在互相平行的对应边上.
分三种情况:
i)如图1,当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,
上时,![]() ,
,![]() ,即
,即![]()
ii)如图2,当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,
上时,![]() ,
,![]() ,即
,即![]()
iii)如图3,当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,
上时,![]() ,
,![]() ,即
,即![]()
综上所述,![]() 与
与![]() 满足的函数关系式是
满足的函数关系式是![]()
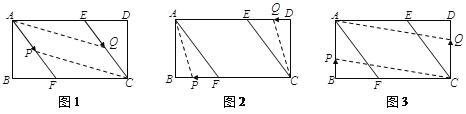
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期学习了一元一次方程的解法,下面是林林同学的解题过程:解方程
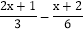 =1
=1解:方程两边同时乘以6,得:
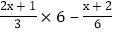 ×6=1×6…………第①步
×6=1×6…………第①步去分母,得:2(2x+1)-x+2=6………………第②步
去括号,得:4x+2-x+2=6…………………第③步
移项,得:4x-x=6-2-2…………………第④步
合并同类项,得:3x=2…………………………第⑤步
系数化1,得:x=
 …………………………第⑥步
…………………………第⑥步上述林林的解题过程从第______步开始出现错误,错误的原因是______.
请你帮林林改正错误,写出完整的解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
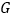 是正方形
是正方形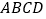 对角线
对角线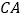 的延长线上任意一点,以线段
的延长线上任意一点,以线段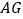 为边作一个正方形
为边作一个正方形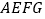 ,线段
,线段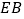 和
和 相交于点
相交于点 .
. (1)求证:
 ;
;(2)判断
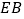 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;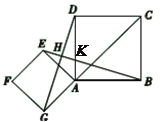
-
科目: 来源: 题型:
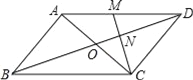
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
 中,
中,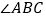 和
和 的平分线交于AD边上一点E,且
的平分线交于AD边上一点E,且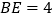 ,
,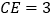 ,则AB的长是( )
,则AB的长是( )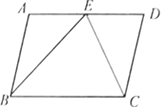
A. 2.5B. 3C. 4D. 2.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

-
科目: 来源: 题型:
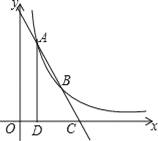
查看答案和解析>>【题目】如图,点A(1,4)、B(2,a)在函数y=
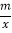 (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
相关试题

