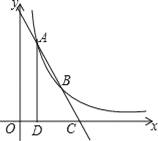
【题目】如图,点A(1,4)、B(2,a)在函数y=![]() (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
参考答案:
【答案】(1)4;(2)C的坐标为(3,0);(3)(﹣2,0).
【解析】试题分析:(1)把点代入求值.(2)先利用反比例函数求出A,B,点坐标,再利用待定系数法求直线方程.(3)假设存在E点,因为![]() ACD是直角三角形,假设
ACD是直角三角形,假设![]() ABE也是直角三角形,利用勾股定理分别计算A,B,C,是直角时AB长度,均与已知矛盾,所以不存在.
ABE也是直角三角形,利用勾股定理分别计算A,B,C,是直角时AB长度,均与已知矛盾,所以不存在.
试题解析:
解:(1)∵点A(1,4)在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1×4=4,
故答案为:4.
(2)∵点B(2,a)在反比例函数y=![]() 的图象上,
的图象上,
∴a==2,
∴B(2,2).
设过点A、B的直线的解析式为y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴过点A、B的直线的解析式为y=﹣2x+6.
当y=0时,有﹣2x+6=0,
解得:x=3,
∴点C的坐标为(3,0).
(3)假设存在,设点E的坐标为(n,0).
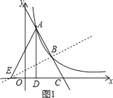
①当∠ABE=90°时(如图1所示),
∵A(1,4),B(2,2),C(3,0),
∴B是AC的中点,
∴EB垂直平分AC,EA=EC=n+3.
由勾股定理得:AD2+DE2=AE2,即42+(x+1)2=(x+3)2,
解得:x=﹣2,
此时点E的坐标为(﹣2,0);
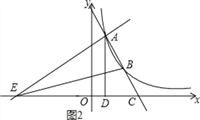
②当∠BAE=90°时,∠ABE>∠ACD,
故△EBA与△ACD不可能相似;
③当∠AEB=90°时,∵A(1,4),B(2,2),
∴AB=![]() ,2>
,2>![]() ,
,
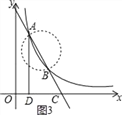
∴以AB为直径作圆与x轴无交点(如图3),
∴不存在∠AEB=90°.
综上可知:在x轴上存在点E,使以A、B、E为顶点的三角形与△ACD相似,点E的坐标为(﹣2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形
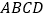 中,
中,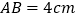 ,
, ,
,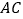 的垂直平分线
的垂直平分线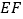 分别交
分别交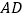 、
、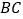 于点
于点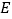 、
、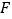 ,垂足为
,垂足为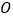 .
.(1)如图,连接
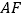 、
、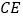 .求证四边形
.求证四边形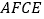 为菱形,并求
为菱形,并求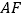 的长;
的长;(2)如图,动点
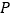 、
、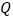 分别从
分别从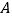 、
、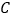 两点同时出发,沿
两点同时出发,沿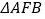 和
和 各边匀速运动一周.即点
各边匀速运动一周.即点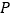 自
自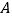 →
→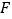 →
→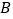 →
→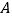 停止,点
停止,点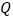 自
自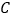 →
→ →
→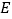 →
→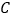 停止.在运动过程中,
停止.在运动过程中,①已知点
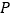 的速度为每秒5
的速度为每秒5 ,点
,点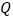 的速度为每秒4
的速度为每秒4 ,运动时间为
,运动时间为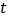 秒,当
秒,当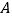 、
、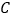 、
、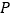 、
、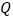 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求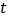 的值.
的值. ②若点
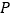 、
、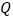 的运动路程分别为
的运动路程分别为 、
、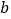 (单位:
(单位: ,
,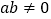 ),已知
),已知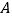 、
、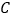 、
、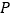 、
、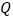 四点为顶点的四边形是平行四边形,写出
四点为顶点的四边形是平行四边形,写出 与
与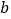 满足的数量关系式.(直接写出答案,不要求证明)
满足的数量关系式.(直接写出答案,不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
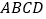 中,
中,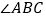 和
和 的平分线交于AD边上一点E,且
的平分线交于AD边上一点E,且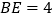 ,
,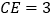 ,则AB的长是( )
,则AB的长是( )
A. 2.5B. 3C. 4D. 2.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班举行了“庆祝建党98周年知识竞赛”活动,班长安排张小明购买奖品,如图两幅图是张小明买回奖品时与班长的对话情况:

请根据图1、图2的信息,解答下列问题:
(1)张小明买了两种笔记本各多少本?(要求列一元一次方程解决问题)
(2)为什么班长说不可能找回68元钱,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

相关试题

