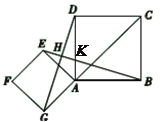
【题目】如图,点![]() 是正方形
是正方形![]() 对角线
对角线![]() 的延长线上任意一点,以线段
的延长线上任意一点,以线段![]() 为边作一个正方形
为边作一个正方形![]() ,线段
,线段![]() 和
和![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
参考答案:
【答案】(1)证明见解析; (2)![]() ,理由见解析.
,理由见解析.
【解析】
(1)由四边形EFGA和四边形ABCD是正方形,易证得△GAD≌△EAB,即EB=GD;
(2)EB⊥GD,由(1)得∠ADG=∠ABE则在△DHK中,∠DHK=90°所以EB⊥GD;
(1)∵四边形ABCD是正方形
∴AB=AD, ∠DAB=90°
∵四边形AEFG是正方形
∴AE=AG, ∠EAG=90°
∴∠DAB=∠EAG
∴∠DAB+∠EAD=∠EAG+∠EAD
即∠BAE=∠DAG
∴![]()
∴![]()
(2)![]()
理由如下:
∵![]()
∴∠ABE=∠ADG
∵∠ABE+∠AKB=90°
∴ ∠ADG+∠AKB=90°
∵∠AKB=∠DKH
∴∠ADG+∠DKH=90°
∴∠DHK=90°
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.

-
科目: 来源: 题型:
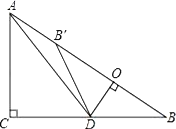
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期学习了一元一次方程的解法,下面是林林同学的解题过程:解方程
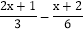 =1
=1解:方程两边同时乘以6,得:
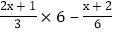 ×6=1×6…………第①步
×6=1×6…………第①步去分母,得:2(2x+1)-x+2=6………………第②步
去括号,得:4x+2-x+2=6…………………第③步
移项,得:4x-x=6-2-2…………………第④步
合并同类项,得:3x=2…………………………第⑤步
系数化1,得:x=
 …………………………第⑥步
…………………………第⑥步上述林林的解题过程从第______步开始出现错误,错误的原因是______.
请你帮林林改正错误,写出完整的解题过程.
-
科目: 来源: 题型:
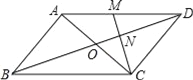
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形
 中,
中,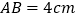 ,
, ,
,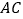 的垂直平分线
的垂直平分线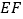 分别交
分别交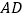 、
、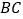 于点
于点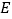 、
、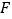 ,垂足为
,垂足为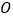 .
.(1)如图,连接
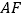 、
、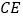 .求证四边形
.求证四边形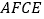 为菱形,并求
为菱形,并求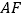 的长;
的长;(2)如图,动点
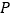 、
、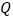 分别从
分别从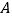 、
、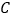 两点同时出发,沿
两点同时出发,沿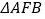 和
和 各边匀速运动一周.即点
各边匀速运动一周.即点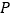 自
自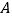 →
→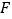 →
→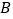 →
→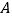 停止,点
停止,点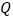 自
自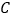 →
→ →
→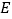 →
→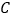 停止.在运动过程中,
停止.在运动过程中,①已知点
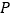 的速度为每秒5
的速度为每秒5 ,点
,点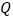 的速度为每秒4
的速度为每秒4 ,运动时间为
,运动时间为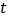 秒,当
秒,当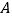 、
、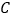 、
、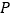 、
、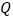 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求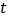 的值.
的值. ②若点
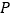 、
、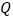 的运动路程分别为
的运动路程分别为 、
、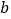 (单位:
(单位: ,
,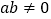 ),已知
),已知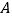 、
、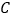 、
、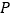 、
、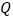 四点为顶点的四边形是平行四边形,写出
四点为顶点的四边形是平行四边形,写出 与
与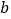 满足的数量关系式.(直接写出答案,不要求证明)
满足的数量关系式.(直接写出答案,不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
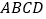 中,
中,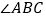 和
和 的平分线交于AD边上一点E,且
的平分线交于AD边上一点E,且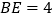 ,
,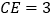 ,则AB的长是( )
,则AB的长是( )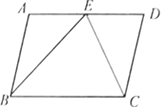
A. 2.5B. 3C. 4D. 2.4
相关试题

