【题目】在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为________cm2.
参考答案:
【答案】126或66
【解析】试题分析:此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
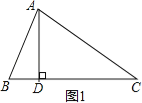
解:当∠B为锐角时(如图1),
在Rt△ABD中,
BD=![]() =
=![]() =5cm,
=5cm,
在Rt△ADC中,
CD=![]() =
=![]() =16cm,
=16cm,
∴BC=21,
∴S△ABC=![]() =
=![]() ×21×12=126cm2;
×21×12=126cm2;
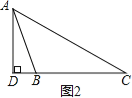
当∠B为钝角时(如图2),
在Rt△ABD中,
BD=![]() =
=![]() =5cm,
=5cm,
在Rt△ADC中,
CD=![]() =
=![]() =16cm,
=16cm,
∴BC=CD﹣BD=16﹣5=11cm,
∴S△ABC=![]() =
=![]() ×11×12=66cm2,
×11×12=66cm2,
故答案为:126或66.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2(x+8)=3x﹣3;
(2)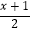 ﹣1=2﹣
﹣1=2﹣ 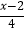 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(1)﹣(﹣2005)=_____
(2)﹣|﹣2018|=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上A、B两点所表示的数分别为﹣2和8.

(1)求线段AB的长;
(2)已知点P为数轴上点A左侧的一点,且M为PA的中点,N为PB的中点. 请你画出图形,观察MN的长度是否发生改变?若不变,求出线段MN的长;若改变,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOD=45°,按下列要求画图并回答问题:
(1)利用三角尺,在直线AB上方画射线OE,使OE⊥AB;
(2)利用圆规,分别在射线OA、OE上截取线段OM、ON,使OM=ON,连接MN;
(3)利用量角器,画∠AOD的平分线OF交MN于点F;
(4)直接写出∠COF=°. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣
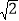 与 是关于1的平衡数;
与 是关于1的平衡数;(2)若(m+
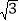 )×(1﹣
)×(1﹣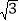 )=﹣5+3
)=﹣5+3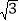 ,判断m+
,判断m+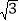 与5﹣
与5﹣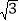 是否是关于1的平衡数,并说明理由.
是否是关于1的平衡数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB、CD相交于点O,OM⊥AB.
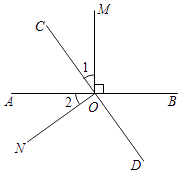
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若∠1= ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.
相关试题

