【题目】如图,已知直线![]() .
.![]() 这两直线之间一点.
这两直线之间一点.
(1)如图1,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

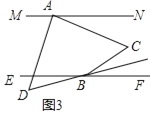
(2)如图2,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并证明你的结论.
有何数量关系?并证明你的结论.
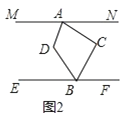
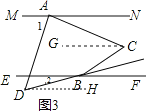
(3)如图3,若![]() 的平分线与
的平分线与![]() 的平分线所在的直线相交于点
的平分线所在的直线相交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
参考答案:
【答案】(1)∠ADB=50°;(2)∠ADB=180°-![]() ∠ACB,证明见解析;(3)∠ADB=90°-
∠ACB,证明见解析;(3)∠ADB=90°-![]() ∠ACB.
∠ACB.
【解析】
(1)如图1,根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠MAC=∠ACG,∠EBC=∠BCG,根据角平分线的定义得到![]() ,即可得到结论;
,即可得到结论;
(2)根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG,根据角平分线的定义得到![]() ,根据平角的定义即可得到结论;
,根据平角的定义即可得到结论;
(3)根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG,根据平行线的定义得到![]() ,根据四边形的内角和和角的和差即可得到结论.
,根据四边形的内角和和角的和差即可得到结论.
(1)如图1,过C作CG∥MN,DH∥MN,
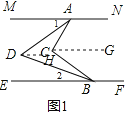
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,
∠MAC=∠ACG,∠EBC=∠BCG,
∵∠MAC与∠EBC的平分线相交于点D,
∴![]() ,
,
∴![]() ;
;
∵∠ACB=100°,
∴∠ADB=50°;
(2)如图2,过C作CG∥MN,DH∥MN,
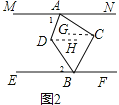
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,
∠NAC=∠ACG,∠FBC=∠BCG,
∵∠MAC与∠EBC的平分线相交于点D,
∴![]()
∴![]()
![]()
![]() ,
,
∴![]() ;
;
(3)如图3,过C作CG∥MN,DH∥MN,
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠
∠NAC=∠ACG,∠FBC=∠BCG,
∵∠MAC与∠FBC的平分线相交于点D,
∴![]()
∵![]()
![]()
![]()
![]() .
.
∴![]()
-
科目: 来源: 题型:
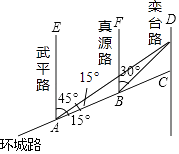
查看答案和解析>>【题目】如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C经测量东方家具城D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°,求C、D之间的距离(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
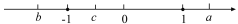
(1)用“<”连接0,a, b, —1
(2)|b-1|+|a-1|=___
(3)化简|a —b|+|a-c|-|b|+|b-c|
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
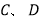 两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往
两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往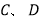 两地,如果从A市运往
两地,如果从A市运往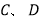 两地运价分别为20元/吨和25元/吨,从B市运往
两地运价分别为20元/吨和25元/吨,从B市运往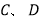 两地运价分别为15元/吨和22元/吨。
两地运价分别为15元/吨和22元/吨。(1)如果A市运往C地的化肥为100吨,则总运费共多少元?
(2)设总运费为
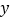 元,如果设A市运往C地的化肥
元,如果设A市运往C地的化肥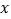 吨,用含
吨,用含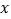 代数式来表示
代数式来表示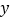 ;
; (3)按照(2)问的要求,猜想
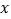 为多少时,总的运费最少,是多少?
为多少时,总的运费最少,是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:① 平方等于64的数是8;② 若a,b互为相反数,ab≠0,则
 ;③ 若
;③ 若 ,则
,则 的值为负数;④ 若ab≠0,则
的值为负数;④ 若ab≠0,则 的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.求证:

(1)AB∥CD;
(2)∠2+∠3=90°.
相关试题

