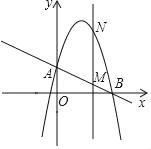
【题目】如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.
(1)求该抛物线的解析式和顶点坐标;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程)
参考答案:
【答案】(1)抛物线解析式为y=﹣x2+![]() x+2;抛物线的顶点坐标为(
x+2;抛物线的顶点坐标为(![]() ,
,![]() );(2)t=2时,MN有最大值,最大值为4;(3)D点坐标为(0,6)或(0,﹣2)或(4,4).
);(2)t=2时,MN有最大值,最大值为4;(3)D点坐标为(0,6)或(0,﹣2)或(4,4).
【解析】分析:(1)把A、B两点坐标代入抛物线y=﹣x2+bx+c得关于b、c方程组,则解方程组即可得到抛物线解析式;然后把一般式配成顶点式得到抛物线的顶点坐标;
(2)先利用待定系数法求出直线AB的解析式为y=﹣![]() x+2,设N(t,﹣t2+
x+2,设N(t,﹣t2+![]() t+2)(0<t<4),则N(t,﹣
t+2)(0<t<4),则N(t,﹣![]() t+2),则MN=﹣t2+
t+2),则MN=﹣t2+![]() t+2﹣(﹣
t+2﹣(﹣![]() t+2),然后利用二次函数的性质解决问题;
t+2),然后利用二次函数的性质解决问题;
(3)由(2)得N(2,5),M(2,1),如图,利用平行四边形的性质进行讨论:当MN为平行四边形的边时,利用MN∥AD,MN=AD=4和确定定义D点坐标,当MN为平行四边形的对角线时,利用AN∥MN,AN=MD和点平移的坐标规律写出对应D点坐标.
详解:(1)把A(0,2)、B(4,0)代入抛物线y=﹣x2+bx+c得![]() ,解得:
,解得:![]() ,∴抛物线解析式为y=﹣x2+
,∴抛物线解析式为y=﹣x2+![]() x+2;
x+2;
∵y=﹣x2+![]() x+2=﹣(x﹣
x+2=﹣(x﹣![]() )2+
)2+![]() ,∴抛物线的顶点坐标为(
,∴抛物线的顶点坐标为(![]() );
);
(2)设直线AB的解析式为y=mx+n,把A(0,2)、B(4,0)代入得:![]() ,解得:
,解得: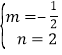 ,∴直线AB的解析式为y=﹣
,∴直线AB的解析式为y=﹣![]() x+2,设N(t,﹣t2+
x+2,设N(t,﹣t2+![]() t+2)(0<t<4),则N(t,﹣
t+2)(0<t<4),则N(t,﹣![]() t+2),∴MN=﹣t2+
t+2),∴MN=﹣t2+![]() t+2﹣(﹣
t+2﹣(﹣![]() t+2)=﹣t2+4t =﹣(t﹣2)2+4,
t+2)=﹣t2+4t =﹣(t﹣2)2+4,
当t=2时,MN有最大值,最大值为4;
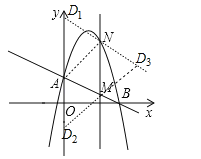
(3)由(2)得N(2,5),M(2,1),如图,当MN为平行四边形的边时,MN∥AD,MN=AD=4,则D1(0,6),D2(0,﹣2),当MN为平行四边形的对角线时,AN∥MN,AN=MD,由于点A向右平移2个单位,再向上平移3个单位得到N点,则点M向右平移2个单位,再向上平移3个单位得到D点,则D3的坐标为(4,4).
综上所述:D点坐标为(0,6)或(0,﹣2)或(4,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MAN=15°,AB=BC=CD=DE=EF,则∠FEM=________.

-
科目: 来源: 题型:
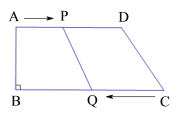
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8
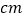 ,AD=24
,AD=24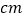 ,BC=26
,BC=26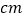 ,点P从点A出发,以1
,点P从点A出发,以1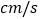 的速度向点D运动;点Q从点C同时出发,以3
的速度向点D运动;点Q从点C同时出发,以3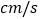 的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为
的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为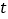
 .
.
(1)
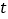 为何值时,四边形PQCD为平行四边形?
为何值时,四边形PQCD为平行四边形?(2)
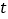 为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等).
为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,D是AB上一点,DE⊥BC于E,ED的延长线交CA的延长线于F,那么△ADF是等腰三角形吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=AC,∠C=90°,AC=7cm,AD是∠BAC的平分线,交BC于D,DE⊥AB于E,求△DEB的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6.
(1)尺规作图:在BC上求作一点P,使点P到点A、B的距离相等;(保留作图痕迹,不写作法和证明)
(2)在(1)的条件下,连接AP,求△APC的周长.
相关试题

