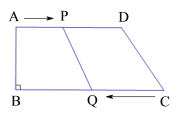
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8![]() ,AD=24
,AD=24![]() ,BC=26
,BC=26![]() ,点P从点A出发,以1
,点P从点A出发,以1![]() 的速度向点D运动;点Q从点C同时出发,以3
的速度向点D运动;点Q从点C同时出发,以3![]() 的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为
的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为![]()
![]() .
.
(1)![]() 为何值时,四边形PQCD为平行四边形?
为何值时,四边形PQCD为平行四边形?
(2)![]() 为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等).
为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等).
参考答案:
【答案】(1)6s;(2)7s
【解析】
(1)根据题意可得PA=t,CQ=3t,则PD=AD-PA=24-t,当PD=CQ时,四边形PQCD为平行四边形,可得方程24-t=3t,解此方程即可求得答案;
(2)过点D作DE⊥BC,则CE=BC-AD=2cm当CQ-PD=4时,四边形PQCD是等腰梯形.即3t-(24-t)=4,求出t的值即可.
(1)运动时间为ts.
AP=t,PD=24-t,CQ=3t,
∵经过ts四边形PQCD平行四边形
∴PD=CQ,即24-t=3t,解得t=6.
当t=6s时,四边形PQCD是平行四边形;
(2)如图,过点D作DE⊥BC,则CE=BC-AD=2cm

∵当CQ-PD=4时,四边形PQCD是等腰梯形.即3t-(24-t)=4,
∴t=7.
∴经过7s四边形PQCD是等腰梯形.
-
科目: 来源: 题型:
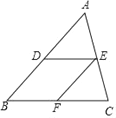
查看答案和解析>>【题目】如图,在△ABC中,D是AB中点,E是AC中点,F是BC中点,请填空:
(1)四边形BDEF是 四边形;
(2)若四边形BDEF是菱形,则△ABC满足的条件是 .
(3)若四边形BDEF是矩形,则△ABC满足的条件是 .
(4)若四边形BDEF是正方形,则△ABC满足的条件是 .
并就(2)、(3)、(4)中选取一个进行证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队承包了某标段全长1800米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进2米,经过5天施工,两组共掘进了60米.
(1)求甲、乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进2米,乙组平均每天能比原来多掘进1米.按此施工进度,能够比原来少用多少天完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MAN=15°,AB=BC=CD=DE=EF,则∠FEM=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,D是AB上一点,DE⊥BC于E,ED的延长线交CA的延长线于F,那么△ADF是等腰三角形吗?为什么?

-
科目: 来源: 题型:
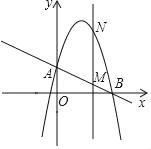
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.
(1)求该抛物线的解析式和顶点坐标;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
相关试题

