Question

【题目】在平面直角坐标系xOy中，点A的坐标为（1，0），P是第一象限内任意一点，连接PO，PA，若∠POA=m°，∠PAO=n°，则我们把（m°，n°）叫做点P 的“双角坐标”．例如，点（1，1）的“双角坐标”为（45°，90°）．
（1）点（ ， ）的“双角坐标”为；
（2）若点P到x轴的距离为 ，则m+n的最小值为 ．

Answer 1

【答案】
（1）（60°，60°）
（2）90
【解析】解：（1）∵P（ ， ），OA=1， ∴tan∠POA= = ，tan∠PAO= = ，
∴∠POA=60°，∠PAO=60°，
即点P的“双角坐标”为（60°，60°），
故答案为：（60°，60°）；
⑵根据三角形内角和定理知若要使m+n取得最小值，即∠POA+∠PAO取得最小值，则∠OPA需取得最大值，如图，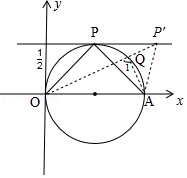

∵点P到x轴的距离为 ，OA=1，
∴OA中点为圆心， 为半径画圆，与直线y= 相切于点P，
在直线y= 上任取一点P′，连接P′O、P′A，P′O交圆于点Q，
∵∠OPA=∠1＞∠OP′A，
此时∠OPA最大，∠OPA=90°，
∴m+n的最小值为90，
故答案为：90．
（1）分别求出tan∠POA、tan∠PAO即可得∠POA、∠PAO的度数，从而得出答案；（2）根据三角形内角和定理知若要使m+n取得最小值，即∠POA+∠PAO取得最小值，则∠OPA需取得最大值，OA中点为圆心， 为半径画圆，与直线y= 相切于点P，由∠OPA=∠1＞∠OP′A知此时∠OPA最大，∠OPA=90°，即可得出答案．