【题目】对于问题:证明不等式a2+b2≥2ab,甲、乙两名同学的作业如下: 甲:根据一个数的平方是非负数可知(a﹣b)2≥0,
∴a2﹣2ab+b2≥0,
∴a2+b2≥2ab.
乙:如图1,两个正方形的边长分别为a、b(b≤a),如图2,先将边长为a的正方形沿虚线部分分别剪成Ⅰ、Ⅱ、Ⅲ三部分,若再将Ⅰ、Ⅱ和边长为b的正方形拼接成如图3所示的图形,可知此时图3的面积为2ab,其面积小于或等于原来两个正方形的面积和,故不等式a2+b2≥2ab成立.
则对于两人的作业,下列说法正确的是( )
A.甲、乙都对
B.甲对,乙不对
C.甲不对,乙对
D.甲、乙都不对
参考答案:
【答案】A
【解析】解:甲的证明利用了完全平方公式和不等式的性质,证明是正确的; 乙的证明:图2:a2=SⅠ+SⅡ+SⅢ ,
图3的面积=2ab=SⅠ+SⅡ+b2 ,
因为SⅢ≥0,
所以SⅠ+SⅡ+SⅢ+b2≥SⅠ+SⅡ+b2
所以a2+b2≥2ab.
故乙的证明也是正确的.
故选A.
【考点精析】根据题目的已知条件,利用不等式的性质的相关知识可以得到问题的答案,需要掌握1:不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变 .2:不等式的两边同时乘以(或除以)同一个 正数 ,不等号的方向 不变 .3:不等式的两边同时乘以(或除以)同一个 负数 ,的方向 改变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ,CD=
,CD=  BC,请求出GE的长.
BC,请求出GE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在已知的△ABC中,按以下步骤作图: ①分别以B,C为圆心,以大于
 BC的长为半径作弧,两弧相交于两点M,N;
BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠B=25°,则∠ACB的度数为( )
A.90°
B.95°
C.100°
D.105° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=a,∠BAC=18°,动点P、Q分别在直线BC上运动,且始终保持∠PAQ=99°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).
(1)点( ,
, 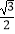 )的“双角坐标”为;
)的“双角坐标”为;
(2)若点P到x轴的距离为 ,则m+n的最小值为 .
,则m+n的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】以下是一位同学所做的实数运算解题过程的一部分. ﹣
 ﹣|﹣1|2017﹣(π﹣3.14)0+4cos60°
﹣|﹣1|2017﹣(π﹣3.14)0+4cos60°
=﹣ +1﹣1+4×
+1﹣1+4×  .
.
(1)指出上面解答过程中的错误,并写出正确的解答过程;
(2)若分式方程 +1=
+1=  的解与(1)中的最终结果相同,求a的值.
的解与(1)中的最终结果相同,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.

(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
相关试题

