【题目】“赵爽炫图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽炫图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为![]() ,较短直角边长为
,较短直角边长为![]() ,若(a+b)2=21,大正方形的面积为13,则小正方形的边长为( )
,若(a+b)2=21,大正方形的面积为13,则小正方形的边长为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】观察图形可知,小正方形的面积=大正方形的面积-4个直角三角形的面积,利用已知(a+b)2=21,大正方形的面积为13,可以得出直角三角形的面积,进而求出小正方形的面积,即可得出小正方形的边长.
解:∵(a+b)2=21,
∴a2+2ab+b2=21,
∵大正方形的面积为13,
2ab=2113=8,
∴小正方形的面积为138=5.
∴小正方形的边长为![]() .
.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】广州市体育中考项目改为耐力跑后,某体育用品商场预测某款运动鞋能够畅销,就用16000元购进了一批这款运动鞋,上市后很快脱销,商场又用40000元购进第二批这款运动鞋,所购数量是第一批的2倍,但每双鞋的进价高了10元.求该款运动鞋第一次进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=5是方程ax﹣8=20+a的解,则a的值是( )
A.2
B.3
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在长方形
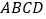 中,
中,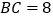 ,
,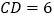 .、点
.、点 在边
在边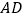 上,将△
上,将△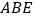 沿着
沿着 折叠,使点
折叠,使点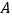 恰好落在对角线
恰好落在对角线 上点
上点 处,则
处,则 的长是___________.
的长是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长分别为4和6,则第三边可能是( )
A. 2 B. 7 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的三个内角的度数分别为40°,60°,80°,则这个三角形是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形
相关试题

