【题目】如图1所示在平面直角坐标系中,有长方形OABC,O是坐标原点,A(a,0),C(0,b),且a,b满足![]()
(1)求A,B,C三点坐标;
(2)如图2所示,长方形对角线OB、AC交于D点,若有一点P从A点出发,以1单位/秒速度向x轴负方向匀速运动,同时另一点Q从O出发,以2个单位/秒,沿长方形边长O-C-B顺时针匀速运动,当Q到达B点时P、Q同时停止运动,设P点开始运动时间为t,请问:当t为何值时有S△OCP≤S△ODQ ?

参考答案:
【答案】(1)A(4,0)B(4,8)C(0,8);(2)![]() ≤t<4或4<t≤5.
≤t<4或4<t≤5.
【解析】
(1)由算术平方根的被开方数为非负数可求得a的值,继而求得b的值,再根据长方形的性质即可求得答案;
(2)分0≤t<4,t=4,4<t≤6三种情况分别讨论即可求得答案.
(1)由![]() ,得
,得
![]() ,
,
解得a=4,
所以b-2=6,
解得b=8,
所以A(4,0),C(0,8),
所以OA=4,OC=8,
又因为ABCD是长方形,
所以AB=OC=8,BC=OA=4,
所以C(4,8);
(2)过D作DE⊥OC于点E,则有DE=2,OE=CE=4,
①当0≤t<4时,如图(1),
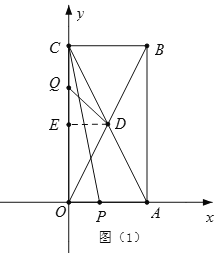
S△OCP=![]() OC·OP=
OC·OP=![]() ×8×(4-t),
×8×(4-t),
S△ODQ=![]() OQ·DE=
OQ·DE=![]() ×2t×2,
×2t×2,
令S△OCP≤S△ODQ,
即有![]() ×8×(4-t)≤
×8×(4-t)≤![]() ×2t×2,
×2t×2,
解得t≥![]() ;
;
②当t=4时,△OPC不存在,舍去;
③当4<t≤6时,如图(2)
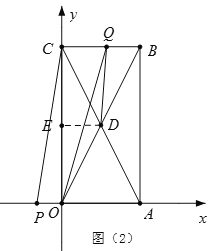
S△OCP=![]() OC·OP=
OC·OP=![]() ×8×(t-4),
×8×(t-4),
S△ODQ=S△OBC-S△OCQ-S△DBQ=![]() OC·BC-
OC·BC-![]() OC·CQ-
OC·CQ-![]() BQ·CE
BQ·CE
=![]() ×4×8-
×4×8-![]() ×8×(2t-8)-
×8×(2t-8)-![]() ×(8+4-2t)×4,
×(8+4-2t)×4,
令S△OCP≤S△ODQ,
即有![]() ×8×(t-4)≤
×8×(t-4)≤![]() ×4×8-
×4×8-![]() ×8×(2t-8)-
×8×(2t-8)-![]() ×(8+4-2t)×4,
×(8+4-2t)×4,
解得 t≤5,
综上所述,当![]() ≤t<4或4<t≤5时成立.
≤t<4或4<t≤5时成立.
-
科目: 来源: 题型:
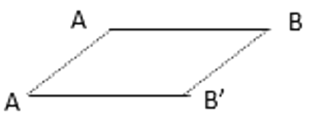
查看答案和解析>>【题目】如图所示,一条线段AB平移一段距离后得到线段A’B’,连接AA’,BB’可以得到一个平行四边形ABB’A’请据此回答下面问题:
在平面直角坐标系中有A点(1,0),B点(-2,1),C点(-1,-3),若坐标平面内存在点D,使得A,B,C,D四点恰好能构成一个平行四边形,求D点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形纸片
 ,
, 为正方形
为正方形 边上的一点(不与点
边上的一点(不与点 ,点
,点 重合).将正方形纸片折叠,使点
重合).将正方形纸片折叠,使点 落在点
落在点 处,点
处,点 落在点
落在点 处,
处, 交
交 于点
于点 ,折痕为
,折痕为 ,连接
,连接 交
交 于点
于点 ,连接
,连接 .下列结论:①
.下列结论:① ;②
;② ;③
;③ 平分
平分 ;④
;④ ;⑤
;⑤ ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣ )2=
)2= 
D.3x2﹣4x﹣2=0化为(x﹣ )2=
)2= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读材料再回答问题.
对三个数x,y,z,规定
 ;
;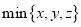 表示x,y,z这三个数中最小的数,如
表示x,y,z这三个数中最小的数,如 ,
,
请用以上材料解决下列问题:
(1)若
 ,求x的取值范围;
,求x的取值范围;(2)①若
 ,求x的值;
,求x的值;②猜想:若
 ,那么a,b,c大小关系如何?请直接写出结论;
,那么a,b,c大小关系如何?请直接写出结论;③问:是否存在非负整数a,b,c使
 等式成立?若存在,请求出a,b,c的值;若不存在,请说明理由.
等式成立?若存在,请求出a,b,c的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(k+1)x2+2(k+1)x+k﹣2=0有实数根,则k的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若α、β为方程2x2﹣5x﹣1=0的两个实数根,则2α2+3αβ+5β的值为( )
A.﹣13
B.12
C.14
D.15
相关试题

