【题目】问题解决:如图1,![]() 中,
中,![]() 为
为![]() 边上的中线,则
边上的中线,则![]() ______
______![]() .
.
问题探究:
(1)如图2,![]() 分别是
分别是![]() 的中线,
的中线,![]() 与
与![]() 相等吗?
相等吗?
解:![]() 中,由问题解决的结论可得,
中,由问题解决的结论可得,![]() ,
,![]() .
.
∴![]()
∴![]()
即![]() .
.
(2)图2中,仿照(1)的方法,试说明![]() .
.
(3)如图3,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中线,则
的中线,则![]() ______
______![]() ,
,![]() ______
______![]() ,
,![]() ______
______![]() .
.

问题拓展:
(1)如图4,![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 的中点,请直接写出阴影部分的面积与四边形
的中点,请直接写出阴影部分的面积与四边形![]() 的面积之间的数量关系:
的面积之间的数量关系:![]() ______
______![]() .
.

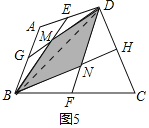
(2)如图5,![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 的中点;请直接写出阴影部分的面积与四边形
的中点;请直接写出阴影部分的面积与四边形![]() 的面积之间的数量关系:
的面积之间的数量关系:![]() ______
______![]() .
.
参考答案:
【答案】问题解决:(1)![]() (2)见解析;(3)
(2)见解析;(3)![]() ,
,![]() ,
,![]() ;
;
问题拓展:(1)![]() ;(2)
;(2)![]() ;
;
【解析】
问题解决:(1)根据中线平方面积即可求解;
(2)根据![]() ,分别减去△BOC的面积即可求解;
,分别减去△BOC的面积即可求解;
(3)根据中线的性质得到各小三角形的面积都相等,即可求解;
问题拓展:(1)连接BD,根据问题解决(1)的结论即可求解;
(2)连接BD,根据问题解决(2)的结论即可求解.
问题解决:(1)∵![]() 中,
中,![]() 为
为![]() 边上的中线,
边上的中线,
∴![]()
![]()
![]() .
.
(2)解:![]() 中,由问题解决的结论可得,
中,由问题解决的结论可得,![]() ,
,![]() .
.
∴![]()
∴![]()
即![]() .
.
(3)∵![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中线,
的中线,
由(2)可得![]()
∴![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() .
.
问题拓展:(1)如图,连接BD,由问题解决(1)的结论得![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
∴![]()
![]()
![]()
![]()
![]()

(2)如图连接BD,根据问题解决(2)的结论得
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=
 ,则tan∠BAD=________.
,则tan∠BAD=________.
【答案】

【解析】延长AD到E,使AD=DE,CF
 ,
,在
 与
与 ,
,,
 ,所以
,所以 ,
,
 是等腰三角形,s
是等腰三角形,s设EM= x,DE=11,MC=10,
 ,
, ,
, x=
x= ,
, tan∠BAD=
tan∠BAD= .
.故答案为
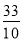 .
.
点睛:倍长中线法构造全等三角形,如图,AD是中线,令AD=DE,则
 ADC全等
ADC全等 EBD.
EBD.
【题型】填空题
【结束】
21【题目】先化简,再求值:
 ÷(
÷( -a+2),其中a=2sin60°+3tan45°.
-a+2),其中a=2sin60°+3tan45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反映的是小丽从家外出到最终回家,离家距离
 (米)与时间
(米)与时间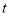 (分)的关系图。请根据图像回答下列问题:
(分)的关系图。请根据图像回答下列问题:(1)小丽在A点表示含义:出发后______分钟时,离家距离______米;
(2)出发后6-10分钟之间可能发生了什么情况:______________________________,出发后14-18分钟之间可能发生了什么情况: ________________________.
(3)在28分钟内的行进过程中,____________段时间的速度最慢,为____________米分;
(4)小丽在回家路上,第28分钟时停了4分钟,之后立即以100米/分的速度回到家.请写出计算过程,并在图中补上28分钟以后的路程
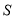 与时间
与时间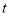 关系图。
关系图。(5)小丽一开始从家外出到最终回家,中途共停留了____________分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,按以下步骤作图:①以点A为圆心,AB的长为半径作弧,交AD于点F;②分别以点F,B为圆心大于
 FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )
FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )
A.12B.20C.24D.48
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
 ÷(
÷( -a+2),其中a=2sin60°+3tan45°.
-a+2),其中a=2sin60°+3tan45°.【答案】﹣
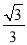 .
.【解析】试题分析:先因式分解,再通分,约分化简,代入数值求值.
试题解析:
解:原式=
 ÷(
÷( -
- )
)=
 ÷
÷ =
= ,
,∵a=2sin60°+3tan45°=2×
 +3×1=
+3×1= +3
+3∴原式=
 =﹣
=﹣ .
.点睛:辨析分式与分式方程
分式,整式A除以整式B,可以表示成的
 的形式.如果B中含有字母,那么称
的形式.如果B中含有字母,那么称  为分式.分式特点是没有等号,分式加减一般需要通分.
为分式.分式特点是没有等号,分式加减一般需要通分.(2)分式方程,分母中含有未知数的方程叫做分式方程.特点是有等号,要先确定最简公分母,去分母的时候要每一项乘以最简公分母,所以一般不需要通分,而且要检验.
【题型】解答题
【结束】
22【题目】图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.

(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:
①∠ABE=∠DCE;②∠AHB=∠EHD;③S△BHE=S△CHD;④AG⊥BE.其中正确的是( )

A.①③B.①②③④C.①②③D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
 (用配方法);
(用配方法);(2)
 ;
;(3)
 ;
;(4)(500-20x)(10+x)=6000.
相关试题

