搜索
【题目】在△ABC中，AB=13，AC=5，BC边上的中线AD=6，点E在AD的延长线上，且AD=DE．
（1）试判断△ABE的形状并说明理由；
（2）求△ABC的面积．
参考答案：
【答案】（1）△ABE是直角三角形；证明见解析；（2）30
【解析】
（1）证明△ACD≌△EBD，得到BE=AC=5，再由AE=12，AB=13，得到∠E=90°，从而得到结论；
（2）由△ACD≌△EBD ，得到S△ABC=S△ABE，从而得到结论．
（1）∵AD为BC边上的中线，∴BD=CD．
在△ACD与△EBD中，∵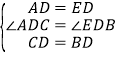
，∴△ACD≌△EBD，∴BE=AC=5．
∵AD=DE=6，∴AE=12．
∵AE2+BE2=52+122=169，AB2=132=169，∴AE2+BE2= AB2，∴∠E=90°，∴△ABE是直角三角形．
（2）∵△ACD≌△EBD ，∴S△ABC=S△ABE=
×EA×BE=×12×5 =30．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以∠AOB的顶点O为圆心，适当长为半径画弧，交OA于点C，交OB于点D，再分别以点C、D为圆心，大于
CD的长为半径画弧，两弧在∠AOB内部交于点E，作射线OE，连接CD.以下说法错误的是（ ）
A. △OCD是等腰三角形 B. 点E到OA、OB的距离相等
C. CD垂直平分OE D. 证明射线OE是角平分线的依据是SSS
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以O为坐标原点在正方形网格中建立直角坐标系，若每个小正方形的边长都为1，网格中有一个格点△ABC(即三角形的顶点都在格点上)．
（1）试在y轴上找一点P，使PC+PB的值最小，请在图中标出P点的位置（留下作图痕迹），并求出PC+PB的最小值；
（2）将△ABC先向下平移3个单位，再向右平移4个单位后得到△A1B1C1，请在图中画出△A1B1C1，并写出点A1的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是边长为2，一个锐角等于60°的菱形纸片，小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合，按顺时针方向旋转三角形纸片，使它的两边分别交CB、BA（或它们的延长线）于点E、F，∠EDF=60°，当CE=AF时，如图1小芳同学得出的结论是DE=DF．
（1）继续旋转三角形纸片，当CE≠AF时，如图2小芳的结论是否成立？若成立，加以证明；若不成立，请说明理由
（2）再次旋转三角形纸片，当点E、F分别在CB、BA的延长线上时，如图3请直接写出DE与DF的数量关系；
（3）连EF，若△DEF的面积为y，CE=x，求y与x的关系式，并指出当x为何值时，y有最小值，最小值是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=ax2+bx﹣3a经过点A（﹣1，0）、C（0，3），与x轴交于另一点B，抛物线的顶点为D．
（1）求此二次函数解析式;
（2）连接DC、BC、DB，求证：△BCD是直角三角形;
（3）在对称轴右侧的抛物线上是否存在点P，使得△PDC为等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读与理解：
折纸，常常能为证明一个命题提供思路和方法．例如，在△ABC中，AB＞AC（如图），怎样证明∠C＞∠B呢？
把AC沿∠A的角平分线AD翻折，因为AB＞AC，所以点C落在AB上的点
处，即
，据以上操作，易证明
≌
，所以
，又因为
>∠B，所以∠C>∠B．感悟与应用：
（1）如图（a），在△ABC中，∠ACB=90°，∠B=30°，CD平分∠ACB，试判断AC和AD、BC之间的数量关系，并说明理由；
（2）如图（b），在四边形ABCD中，AC平分∠BAD，AC=16，AD=8，DC=BC=12，
① 求证：∠B+∠D=180°；
② 求AB的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰梯形ABCD中，AD∥BC，CA平分∠BCD，∠B=60°，若AD=3，则梯形ABCD的周长为（ ）
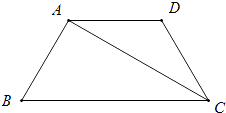
A.12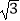
B.15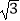
C.12
D.15
相关试题
