Question

【题目】如图，四边形ABCD是边长为2，一个锐角等于60°的菱形纸片，小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合，按顺时针方向旋转三角形纸片，使它的两边分别交CB、BA（或它们的延长线）于点E、F，∠EDF=60°，当CE=AF时，如图1小芳同学得出的结论是DE=DF．

（1）继续旋转三角形纸片，当CE≠AF时，如图2小芳的结论是否成立？若成立，加以证明；若不成立，请说明理由
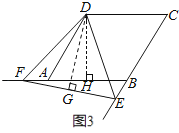
（2）再次旋转三角形纸片，当点E、F分别在CB、BA的延长线上时，如图3请直接写出DE与DF的数量关系；
（3）连EF，若△DEF的面积为y，CE=x，求y与x的关系式，并指出当x为何值时，y有最小值，最小值是多少？

Answer 1

【答案】
（1）

解：DF=DE．理由如下：

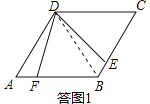
如答图1，连接BD．

∵四边形ABCD是菱形，

∴AD=AB．

又∵∠DAB=60°，

∴△ABD是等边三角形，

∴AD=BD，∠ADB=60°，

∴∠DBE=∠DAF=60°

∵∠EDF=60°，

∴∠ADF=∠BDE．∵在△ADF与△BDE中，，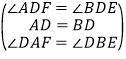

∴△ADF≌△BDE（ASA），

∴DF=DE；

（2）

解：DF=DE．理由如下：

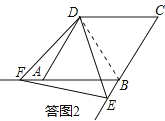
如答图2，连接BD．∵四边形ABCD是菱形，

∴AD=AB．

又∵∠DAB=60°，

∴△ABD是等边三角形，

∴AD=BD，∠ADB=60°，

∴∠DBE=∠DAF=60°

∵∠EDF=60°，

∴∠ADF=∠BDE．

∵在△ADF与△BDE中，，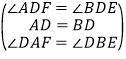

∴△ADF≌△BDE（ASA），

∴DF=DE；

（3）

解：

由（2）知，DE=DF，又∵∠EDF=60°，

∴△DEF是等边三角形，

∵四边形ABCD是边长为2的菱形，

∴DH=，

∵BF=CE=x，

∴AF=x﹣2，

∴FH=AF+AH=x﹣2+1=x﹣1，

∴DF==，DG=×，

∴y=S△DEF=×EF×DG=×××=（x﹣1）2+．

∴当x=1时，y最小值=．

【解析】（1）如答图1，连接BD．根据题干条件首先证明∠ADF=∠BDE，然后证明△ADF≌△BDE（ASA），得DF=DE；
（2）如答图2，连接BD．根据题干条件首先证明∠ADF=∠BDE，然后证明△ADF≌△BDE（ASA），得DF=DE；
（3）根据（2）中的△ADF≌△BDE得到：△DEF是等边三角形，AF=BE．所以要表示△DEF的面积需要用含x的代数式把底EF和高DG表示出来.据此列出y关于x的二次函数，通过求二次函数的最值来求y的最小值．