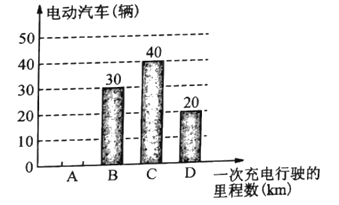
【题目】为了了解某种电动汽车的性能,某机构对这种电动汽车进行抽检,获得如图中不完整的统计图,其中![]() ,
,![]() ,
,![]() ,
,![]() 表示 一次充电后行驶的里程数分别为
表示 一次充电后行驶的里程数分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
电动汽车一次充电后行驶里程数的条形统计图
电动汽车一次充电后行驶里程数的扇形统计图
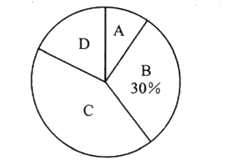
(2)求扇形统计图中表示一次充电后行驶路为![]() 的扇形圆心角的度数;
的扇形圆心角的度数;
(3)估计这种电动汽车一次充电后行驶的平均里程多少![]() ?
?
参考答案:
【答案】(1)总共有![]() 辆.
辆.![]() 类有10辆,图略;(2)72°;(3)这种电动汽车一次充电后行驶的平均里程数为
类有10辆,图略;(2)72°;(3)这种电动汽车一次充电后行驶的平均里程数为![]() 千米.
千米.
【解析】
(1)根据条形统计图和扇形图可知,将一次充电后行驶的里程数分为B等级的有30辆电动汽车,所占的百分比为30%,用30÷30%即可求出这次被抽检的电动汽车总量,再分别减去B、C、D等级的辆数,得到A等级的辆数,即可补全条形图;
(2)用D等级的辆数除以汽车总量,得到其所占的百分比,再乘以360°得到扇形圆心角的度数;
(3)用总里程除以汽车总辆数,即可解答.
解:(1)这次被抽检的电动汽车共有30÷30%=100(辆).
A等级汽车数量为:100-(30+40+20)=10(辆).
条形图补充如下:

(2)D等级对应的圆心角度数为![]() .
.
(3)![]() .
.
答:这种电动汽车一次充电后行驶的平均里程数为![]() 千米.
千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=
 的图象的两个交点.
的图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A、B、C三点,点A和点B间距20个单位长度且点A、B表示的有理数互为相反数,AC=36,数轴上有一动点P从点A出发,以每秒1个单位长度的速度沿数轴向终点C移动,设移动时间为t秒.
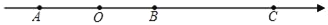
(1)点A表示的有理数是 ,点B表示的有理数是 ,点C表示的有理数是 .
(2)当点P运动到点B时,点Q从点O出发,以每秒6个单位长度的速度沿数轴在点O和点C之间往复运动.
①求t为何值时,点Q第一次与点P重合?
②当点P运动到点C时,点Q的运动停止,求此时点Q一共运动了多少个单位长度,并求出此时点Q在数轴上所表示的有理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一张边长为
 的正方形纸片
的正方形纸片 ,点
,点 为正方形
为正方形 边上的一点(不与点
边上的一点(不与点 ,点
,点 重合)将正方形纸片折叠,使点
重合)将正方形纸片折叠,使点 落在
落在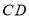 边上的
边上的 处,点
处,点 落在
落在 处,
处, 交
交 于
于 ,折痕为
,折痕为 ,连接
,连接 ,
, .则
.则 的周长是______.
的周长是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.
(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作ADEF.
①ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某童装网店批发商批发一种童装,平均每天可售出
 件,每件盈利
件,每件盈利 元.经调查,如果每件童装降价
元.经调查,如果每件童装降价 元,那么平均每天就可多售出
元,那么平均每天就可多售出 件.
件. (1)设每件童装降价
 元,那么每天可售出多少件童装?每件童装的利润是多少元?(用含
元,那么每天可售出多少件童装?每件童装的利润是多少元?(用含 的代数式表示)
的代数式表示)(2)为了迎接“六一”儿童节,商家决定降价促销、尽快减少库存,又想保证平均每天盈利
 元,求每件童装应降价多少元?
元,求每件童装应降价多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算下列各题:
①2x2﹣4x+1+2x﹣5x2
②(8x﹣3x2)﹣5xy﹣2(3xy﹣2x2)
(2)先化简,再求值:(3x2y+5x)﹣[x2y﹣4(x﹣x2y)],其中(x+2)2+|y﹣3|=0
相关试题

