【题目】如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.
(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作ADEF.
①ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.

参考答案:
【答案】(1)不存在;(2)①存在,6![]() ;②3.
;②3.
【解析】试题分析:(1)根据等边三角形的性质可知: ![]() 由三角形外角的性质可知
由三角形外角的性质可知![]() 从而可知:
从而可知: ![]() 所以
所以![]() 点E不能移动到直线AB上.
点E不能移动到直线AB上.
(2)因为△ADE的面积![]() 所以当AD最短时,△ADE的面积有最小,根据垂线段最短可知当AD⊥BC时,△ADE的面积最小.四边形
所以当AD最短时,△ADE的面积有最小,根据垂线段最短可知当AD⊥BC时,△ADE的面积最小.四边形![]() 为平四边形,AE为对角线,所以平行四边形
为平四边形,AE为对角线,所以平行四边形![]() 的面积是△ADE面积的2倍,所以△ADE的面积最小时,平行四边形的面积最小;
的面积是△ADE面积的2倍,所以△ADE的面积最小时,平行四边形的面积最小;
(3)当点N、M、P在一条直线上,且NP⊥AD时,MN+MP有最小值,最小值为AD与EF之间的距离.
试题解析:(1)不存在.
理由:如图1所示:
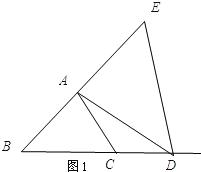
∵△ABC和△ADE均为等边三角形,
∴![]()
∵![]()
∴![]()
又∵![]()
∴![]()
∴点E不能移动到直线AB上.
(2)①存在:在图(2)中,当AD⊥BC时,△ADE的面积最小.
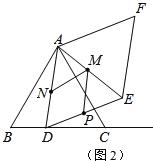
在Rt△ADB中, ![]()
∴△ADE的面积![]()
∵四边形ADEF为平四边形,AE为对角线,
∴平行四边形ADEF的面积是△ADE面积的2倍.
∴ADEF的面积的最小值![]()
②如图3所示:作点P关于AE的对称点P1,
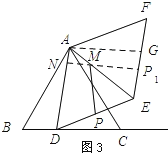
当点N、M、P在一条直线上,且NP⊥AD时,
过点A作AG∥NP1,
∵AN∥GP1,AG∥NP1,
∴四边形ANP1G为平行四边形.
∴![]()
即MN+MP的最小值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
网购达人
非网购达人
合计
男性
30
女性
12
30
合计
60
若网购金额超过2千元的顾客称为“网购达人”,网购金额不超过2千元的顾客称为“非网购达人”.
(Ⅰ)若抽取的“网购达人”中女性占12人,请根据条件完成上面的2×2列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
(Ⅱ)该营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定12人,若需从这12人中随机选取3人进行问卷调查.设ξ为选取的3人中“网购达人”的人数,求ξ的分布列和数学期望.
(参考公式: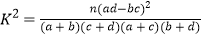 ,其中n=a+b+c+d)
,其中n=a+b+c+d)P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,BD=2AD=8,AB=4
 .
. 
(Ⅰ)证明:平面PBD⊥平面PAD;
(Ⅱ)求二面角B﹣PA﹣D的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
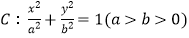 的离心率为
的离心率为 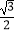 ,过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,斜率为k(k≠0)的直线l过点(1,0),且与椭圆C相交于不同的两点A,B.
,过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,斜率为k(k≠0)的直线l过点(1,0),且与椭圆C相交于不同的两点A,B.
(Ⅰ)求椭圆C的方程;
(Ⅱ)在x轴上是否存在点M,使得无论k取何值,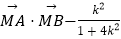 为定值?若存在,求出点M的坐标;若不存在,请说明理由.
为定值?若存在,求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx﹣mx的图象与直线y=﹣1相切. (Ⅰ)求m的值,并求f(x)的单调区间;
(Ⅱ)若g(x)=ax3 , 设h(x)=f(x)﹣g(x),讨论函数h(x)的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
 ,直线l的参数方程为
,直线l的参数方程为  (t为参数),直线l与曲线C1交于A,B两点. (Ⅰ)求|AB|的长度;
(t为参数),直线l与曲线C1交于A,B两点. (Ⅰ)求|AB|的长度;
(Ⅱ)若曲线C2的参数方程为 (α为参数),P为曲线C2上的任意一点,求△PAB的面积的最小值.
(α为参数),P为曲线C2上的任意一点,求△PAB的面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )

A.4.5
B.6
C.7.5
D.9
相关试题

