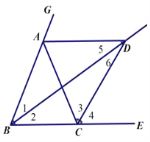
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)∠BDC=![]() ∠BAC,证明见解析
∠BAC,证明见解析
【解析】
(1)根据平行线的性质得到∠ADB=∠DBC,由角平分线的定义得到∠ABD=∠DBC,等量代换得到∠ABD=∠ADB,根据等腰三角形的判定即可得到AB=AD;(2)根据平行线的性质得到∠ADC=∠DCE,由①知AB=AD,等量代换得到AC=AD,根据等腰三角形的性质得到∠ACD=∠ADC,求得∠ACD=∠DCE,即可得到结论;
(3)根据角平分线的定义得到∠DBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+
∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+![]() ∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ABC+
∠ABC+![]() ∠BAC,即可得到结论.
∠BAC,即可得到结论.
证明:
![]() (1) AD∥BE
(1) AD∥BE
![]() ∠2= ∠5
∠2= ∠5
![]() AD平分∠GBE
AD平分∠GBE
![]() ∠2= ∠1
∠2= ∠1
![]() ∠1= ∠5 , AB= AD
∠1= ∠5 , AB= AD
(2) ![]() AB= AD AB= ACAC= AD
AB= AD AB= ACAC= AD
![]() ∠3= ∠ADC
∠3= ∠ADC
![]() 又AD∥BE ∠ADC= ∠4
又AD∥BE ∠ADC= ∠4
![]() ∠3= ∠4
∠3= ∠4
![]() CD平分∠ACE
CD平分∠ACE
(3)∠BDC=![]() ∠BAC
∠BAC
![]()
![]() 证明:BD平分∠ABE
证明:BD平分∠ABE
∴∠2= ∠1 = ![]() ∠ABC
∠ABC
∠1+ ∠2+ ∠BAC=∠4 +∠3①
①式两边除以2得![]() ∠BAC=∠4-∠2
∠BAC=∠4-∠2
而由∠2+ ∠6 =∠4 得出∠6 =∠4 -∠2 即∠BDC=∠4 -∠2
∠BDC=![]() ∠BAC
∠BAC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,关于点
 的图象变化有以下说法:
的图象变化有以下说法:①点
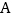 关于
关于 轴的对称点
轴的对称点 的坐标为
的坐标为
②点
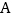 与点
与点 关于原点对称
关于原点对称③把点
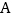 先向右平移
先向右平移 个单位长度,再向下平移
个单位长度,再向下平移 个单位长度得到点
个单位长度得到点
④把点
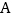 绕原点顺时针旋转
绕原点顺时针旋转 ,得到点
,得到点
其中,正确的说法是( )
A. ①③④ B. ①②③④ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的
 个棋子组成轴对称图形,白棋的
个棋子组成轴对称图形,白棋的 个棋子也成轴对称图形.则下列下子方法不正确的是( ),
个棋子也成轴对称图形.则下列下子方法不正确的是( ), .
.
A. 黑(3,7);白(5,3) B. 黑(4,7);白(6,2)
C. 黑(2,7);白(5,3) D. 黑(3,7);白(2,6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是锐角三角形
是锐角三角形 内一点,
内一点, ,
,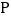 是
是 内不同于
内不同于 的另一点;
的另一点; 、
、 分别由
分别由 、
、 逆时针旋转而得,旋转角都为
逆时针旋转而得,旋转角都为 ,则下列结论:
,则下列结论:①
 .
.②
 、
、 、
、 、
、 在一条直线上.
在一条直线上.③
 .
.④
 .
.其中正确的有( )
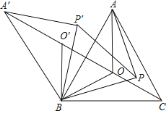
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在等边三角形
 中,
中, 是
是 边上的动点,以
边上的动点,以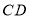 为一边,向上作等边三角形
为一边,向上作等边三角形 ,连接
,连接 .
.(1)
 和
和 全等吗?请说明理由;
全等吗?请说明理由;(2)试说明:
 ;
;(3)如图(2),将动点
 运动到边
运动到边 的延长线上,所作三角形
的延长线上,所作三角形 仍为等边三角形,请问是否仍有
仍为等边三角形,请问是否仍有 ?请说明理由.
?请说明理由.
相关试题

