【题目】图中是一副三角板，45°的三角板 Rt△DEF 的直角顶点 D 恰好在 30°的三角板 Rt△ABC 斜边 AB 的中点处，∠A＝30°，∠E＝45°，∠EDF＝∠ACB＝90°，DE 交 AC 于点 G，GM⊥AB 于 M．
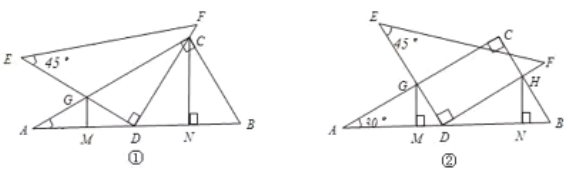
（1）如图①，当 DF 经过点 C 时，作 CN⊥AB 于 N，求证：AM＝DN；
（2）如图②，当 DF∥AC 时，DF 交 BC 于 H，作 HN⊥AB 于 N，（1）的结论仍然成立，请你说明理由．
【答案】（1）见详解；（2）见详解
【解析】
根据题干可推知,本题主要考查了特殊三角形的判定及性质.
(1)根据指教三角形斜边的中线的性质,先证出△BCD是等边三角形，再利用等腰三角形三线合一的定理，可得出DN=
BD，∠ADG=30°, 那么△ADG是等腰三角形，可得出AM=AD,所以可证出AM=DN;
(2)根据全等三角形的判定定理及性质定理,先证△ADG≌△DBH,在此基础上再证△AGM≌△DHN,从而得出AM=DN.
(1)证明:∵∠ACB= 90°，D是AB的中点，
∴CD= AD= BD
又∵∠B=90°-∠A=60°,
∴△BCD是等边三角形,
又∵CN⊥DB，
∴DN=BD,
∵∠EDF=90°，△BCD是等边三角形，
∴∠ADG= 30°,而∠A = 30°,
∴GA = GD,
∵GM⊥AB，
∴AM=AD;
又∵AD=DB，
∴AM = DN.
故AM = DN得证.
(2) (1)的结论仍然成立，理由如下
∵DF//AC,
∴∠1=∠A =30°,∠AGD=∠GDH =90°,
∴∠ADG = 60°.
∵∠B=60° ,AD= DB,
∴△ADG≌△DBH,
∴ AG= DH.
又∵∠1= ∠A, GM⊥AB , HN⊥AB,
∴△AMG≌△DNH，
∴ AM= DN.
故(1)的结论仍然成立.
天天练口算系列答案科目：初中数学 来源： 题型：
【题目】一项工程，甲、乙两公司合做，12天可以完成，共需付工费102000元；如果甲、乙两公司单独完成此项公程，乙公司所用时间是甲公司的1.5倍，乙公司每天的施工费比甲公司每天的施工费少1500元。
（1）甲、乙公司单独完成此项工程，各需多少天？
（2）若让一个公司单独完成这项工程，哪个公司施工费较少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命，令人痛心疾首．今年某校为确保学生安全，开展了“远离溺水珍爱生命”的防溺水安全知识竞赛．现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：A．80≤x＜85，B．85≤x＜90，C．90≤x＜95，D．95≤x≤100），下面给出了部分信息：七年级10名学生的竞赛成绩是：99，80，99，86，99，96，90，100，89，82；八年级10名学生的竞赛成绩在C组中的数据是：94，90，94.
七、八年级抽取的学生竞赛成绩统计表
年级 | 七年级 | 八年级 |
平均数 | 92 | 92 |
中位数 | 93 | b |
众数 | c | 100 |
方差 | 52 | 50.4 |
根据以上信息，解答下列问题：
（1）直接写出上述图表中a，b，c的值；
（2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好？请说明理由（一条理由即可）；
（3）该校七、八年级共720人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（x≥90）的学生人数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，一个点从原点O出发，按向右→向上→向右→向下的顺序依次不断移动，每次移动1个单位，其移动路线如图所示，第1次移到点A1，第二次移到点A2，第三次移到点A3，…，第n次移到点An，则点A2019的坐标是_____________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一张方桌由1个桌面，4条桌腿组成，如果1m3木料可以做方桌的桌面50个或做桌腿300条，现有25m3木料，那么用多少m3的木料做桌面，多少m3的木料做桌腿，做出的桌面与桌腿，恰好能配成方桌?能配成多少张方桌.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算:
（1）
(2) 
(3) 
(4) 
【答案】(1) 
;(2) 
;(3) 
; (4) 
【解析】试题分析：（1）分子、分母分解因式后约分即可；
（2）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可；
（3）第二个分式分子、分母分解因式后约分，然后通分转化为同分母分式，最后依照同分母分式的加减法则计算即可；
（4）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可．
试题解析：
解：（1）原式＝
＝
；
（2）原式＝
＝
＝
；
（3）原式＝
＝
＝
＝
＝
；
（4）原式＝
＝
＝
．
点睛：此题考查了分式的混合运算，熟练掌握运算法则和运算顺序是解本题的关键．
【题型】解答题
【结束】
20
【题目】解分式方程：
(1) 
(2) 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t分后甲、乙两遥控车与B处的距离分别为d1,d2(单位:米),则d1,d2与t的函数关系如图,试根据图象解决下列问题.
（1）填空：乙的速度v2=________米/分;
（2）写出d1与t的函数表达式;
（3）若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探究什么时间两遥控车的信号不会产生相互干扰?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
