【题目】如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是 . 随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是 . 
参考答案:
【答案】( ![]() ,1);y=
,1);y= ![]() x﹣2
x﹣2
【解析】解:如图,过点C′作C′F⊥x轴于点F,
∵△AOC′是等边三角形,OA=2,
∴C′F=1.
在Rt△OC′F中,
由勾股定理,得OF= ![]() =
= ![]() =
= ![]() .
.
∴点C′的坐标为( ![]() ,1).
,1).
∵△AOC′与△ABC都是等边三角形,
∴AO=AC′,AB=AC,∠BAC=∠OAC′=60°,
∴∠BAC﹣∠OAC=∠OAC′﹣∠OAC,
∴∠BAO=∠CAC′,
在△AOB与△AC′C中,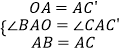
∴△AOB≌△AC′C(SAS).
∴∠BOA=∠CC′A=90°,
∴点C在过点C′且与AC垂直的直线上,
∵点A的坐标是(0,2),△ABC是等边三角形,
∴点C移动到y轴上的坐标是(0,﹣2),
设点C所在的直线方程为:y=kx+b(k≠0).把点( ![]() ,1)和(0,﹣2)分别代入,得
,1)和(0,﹣2)分别代入,得 ![]() ,
,
解得 ![]() ,
,
所以点C移动所得图象的解析式是为:y= ![]() x﹣2.
x﹣2.
所以答案是( ![]() ,1),y=
,1),y= ![]() x﹣2.
x﹣2.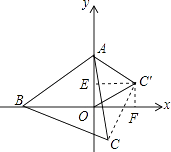
-
科目: 来源: 题型:
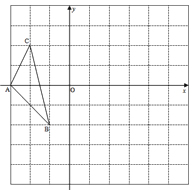
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:A(-3,0),B(-1,-2),C(-2,2).
(1)请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.
(2)请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=mx﹣4m(m是常数,且m≠0)的图象分别交x轴、y轴于点M,N,线段MN上两点A,B(点B在点A的右侧),作AA1⊥x轴,BB1⊥x轴,且垂足分别为A1 , B1 , 若OA1+OB1>4,则△OA1A的面积S1与△OB1B的面积S2的大小关系是( )

A.S1>S2
B.S1=S2
C.S1<S2
D.不确定的 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′是直线y=
 x上一点,则点B与其对应点B′间的距离为 .
x上一点,则点B与其对应点B′间的距离为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示,你认为商家更应该关注鞋子尺码的( )
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
4
6
6
10
2
1
1
A.平均数 B.中位数 C.众数 D.方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 中位数就是一组数据中最中间的一个数
B. 8,9,9,10,10,11这组数据的众数是9
C. 如果x1,x2,x3,…,xn的平均数是x,那么(x1-x)+(x2-x)+…+(xn-x)=0
D. 一组数据的方差是这组数据的平均数的平方
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 经过A(-1,0),B(3,0),C(0,3)三点,直线是抛物线的对称轴.
经过A(-1,0),B(3,0),C(0,3)三点,直线是抛物线的对称轴.(1)求抛物线的函数解析式及顶点D的坐标;
(2)设点P是直线上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线上是否存在点M,使△MAC为等腰三角形?若存在,求出所有符合条件的点M的坐标,若不存在,请说明理由.

相关试题

