搜索
【题目】如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A′是直线y= 
x上一点，则点B与其对应点B′间的距离为 ． 
参考答案：
【答案】5
【解析】解：如图，连接AA′、BB′．
∵点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，
∴点A′的纵坐标是4．
又∵点A的对应点在直线y= 
x上一点，
∴4= x，解得x=5．
∴点A′的坐标是（5，4），
∴AA′=5．
∴根据平移的性质知BB′=AA′=5．
故答案为：5．
根据平移的性质知BB′=AA′．由一次函数图象上点的坐标特征可以求得点A′的坐标，所以根据两点间的距离公式可以求得线段AA′的长度，即BB′的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校10名篮球运动员的年龄情况，统计如下表：
年龄/岁
12
13
14
15
人数/名
2
4
3
1
则这10名篮球运动员年龄的中位数为( )
A. 12 B. 13 C. 13.5 D. 14
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，图中的小方格都是边长为1的正方形，△ABC的顶点坐标分别为：A（-3，0），B（-1，-2），C（-2，2）．
（1）请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.
（2）请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.
-
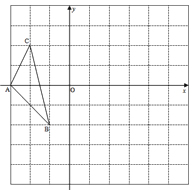
科目： 来源： 题型：
查看答案和解析>>【题目】如图，函数y=mx﹣4m（m是常数，且m≠0）的图象分别交x轴、y轴于点M，N，线段MN上两点A，B（点B在点A的右侧），作AA1⊥x轴，BB1⊥x轴，且垂足分别为A1 ， B1 ， 若OA1+OB1＞4，则△OA1A的面积S1与△OB1B的面积S2的大小关系是（ ）
A.S1＞S2
B.S1=S2
C.S1＜S2
D.不确定的 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，点A的坐标是（0，2），点B是x轴上的一个动点，始终保持△ABC是等边三角形（点A、B、C按逆时针排列），当点B运动到原点O处时，则点C的坐标是 ． 随着点B在x轴上移动，点C也随之移动，则点C移动所得图象的解析式是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一家鞋店在一段时间内销售了某种女鞋30双，各种尺码的销售量如下表所示，你认为商家更应该关注鞋子尺码的（ ）
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
4
6
6
10
2
1
1
A.平均数 B.中位数 C.众数 D.方差
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是( )
A. 中位数就是一组数据中最中间的一个数
B. 8，9，9，10，10，11这组数据的众数是9
C. 如果x1，x2，x3，…，xn的平均数是x，那么(x1－x)＋(x2－x)＋…＋(xn－x)＝0
D. 一组数据的方差是这组数据的平均数的平方
相关试题
