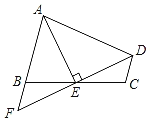
【题目】如图,在四边形ABCD中,AB∥DC,E为BC的中点,连接DE、AE,AE⊥DE,延长DE交AB的延长线于点F.若AB=5,CD=3,则AD的长为_____.
参考答案:
【答案】8
【解析】
首先由E为BC的中点,得出BE=EC,又由AB∥CD,得出∠F=∠CDE,且∠BEF=∠CED,BE=EC,进而判定△BEF≌△CED(AAS),得出EF=DE,BF=CD,进而得出AF,最后由AE⊥DE,EF=DE,即可得出AD.
∵E为BC的中点,
∴BE=EC,
∵AB∥CD,
∴∠F=∠CDE,且∠BEF=∠CED,BE=EC,
∴△BEF≌△CED(AAS)
∴EF=DE,BF=CD=3,
∴AF=AB+BF=8,
∵AE⊥DE,EF=DE,
∴AF=AD=8.
-
科目: 来源: 题型:
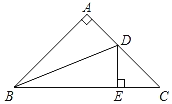
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=12,则△DEC的周长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程时,配方正确的是( )
A. 方程x2-6x-5=0,可化为(x-3)2=4
B. 方程y2-2y-2 015=0,可化为(y-1)2=2 015
C. 方程a2+8a+9=0,可化为(a+4)2=25
D. 方程2x2-6x-7=0,可化为

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)6a(a﹣2)﹣(2﹣3a)2;
(2)(2x2﹣3y)(2x2+3y)﹣2x(﹣3x3);
(3)先化简,再求值:[2(x﹣y)]2﹣(12x3y2﹣18x2y3)÷(3xy2),其中x=﹣3,y=﹣
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级
成绩(分)
频数(人数)
A
36<x≤40
19
B
32<x≤36
b
C
28<x≤32
5
D
24<x≤28
4
E
20<x≤24
2
合计
a
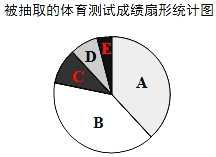
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.
-
科目: 来源: 题型:
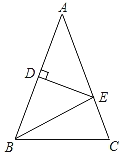
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=14,DE是线段AB的垂直平分线.
(1)若△EBC的周长是24,求BC的长;
(2)若∠A=x°,求∠EBC的度数(用含x的代数式表示).
相关试题

