【题目】如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.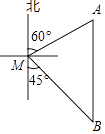
(1)求渔船从B到A的航行过程中与码头M之间的最小距离.
(2)若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.
参考答案:
【答案】
(1)解:作AC⊥AB于C, 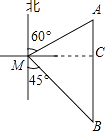
则MC=BM×cos45°=60 ![]() 海里,
海里,
答:渔船从B到A的航行过程中与码头M之间的最小距离为60 ![]() 海里
海里
(2)解:在Rt△ACM中,AM= ![]() =40
=40 ![]() ,
,
40 ![]() ÷20=2
÷20=2 ![]() ,
,
答:渔船从A到达码头M的航行时间为2 ![]() 小时.
小时.
【解析】(1)作AC⊥AB于C, 在Rt△MBC中利用余弦定义得出MC=BM×cos45°即可;(2)在Rt△ACM中,利用利用余弦定义得出AM的长度,再用AM的长度除以渔船的航行速度即可。
【考点精析】认真审题,首先需要了解关于方向角问题(指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
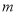 ,
,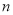 满足等式
满足等式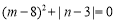 .
.(1)求
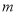 ,
,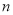 的值;
的值;(2)已知线段
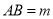 ,在直线
,在直线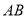 上取一点
上取一点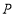 ,恰好使
,恰好使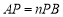 ,点
,点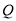 为
为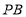 的中点,求线段
的中点,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图时用黑色的正六边形和白色的正方形按照一定的规律组合而成的两色图案

(1)当黑色的正六边形的块数为1时,有6块白色的正方形配套;当黑色的正六边形块数为2时,有11块白色的正方形配套;则当黑色的正六边形块数为3,10时,分别写出白色的正方形配套块数;
(2)当白色的正方形块数为201时,求黑色的正六边形的块数.
(3)组成白色的正方形的块数能否为100,如果能,求出黑色的正六边形的块数,如果不能,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是两位同学的一段对话:
聪聪:周末我们去国家博物馆参观“伟大的变革﹣﹣庆祝改革开放40周年大型展览”吧.
明明:好啊,我家离国家博物馆约30km,我坐地铁先走,地铁的平均行驶速度是公交车的1.5倍呢.
聪聪:嗯,我周末住奶奶家,离国家博物馆只有5km,坐公交车,你出发40分钟后我再出发就能和你同时到达.
根据对话内容,请你求出公交车和地铁的平均行驶速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】凤凰景区的团体门票的价格规定如下表
购票人数
1~55
56~110
111~165
165以上
价格(元/人)
10
9
8
7
某校七年级(1)班和(2)班共112人去凤凰景区进行研学春游活动,当两班都以班为单位分别购票,则一共需付门票1060元.
(1)你认为由更省钱的购票方式吗?如果有,能节省多少元?
(2)若(1)班人数多于(2)班人数,求(1)(2)班的人数各是多少?
(3)若七年级(3)班53人也一同前去春游时,如何购票显得更为合理?请你设计一种更省钱的方案,并求出七年级3个班共需付门票多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BC=5,AB=1,AB⊥BC,射线CM⊥BC,动点P在线段BC上(不与点B,C重合),过点P作DP⊥AP交射线CM于点D,连接AD.
(1)如图1,若BP=4,判断△ADP的形状,并加以证明.
(2)如图2,若BP=1,作点C关于直线DP的对称点C′,连接AC′.
①依题意补全图2;
②请直接写出线段AC′的长度.

-
科目: 来源: 题型:
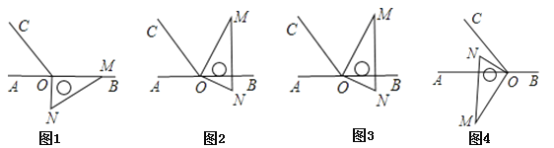
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)求∠CON的度数;
(2)如图2是将图1中的三角板绕点O按每秒15°的速度沿逆时针方向旋转一周的情况,在旋转的过程中,第t秒时,三条射线OA、OC、OM构成两个相等的角,求此时的t值
(3)将图1中的三角板绕点O顺时针旋转至图3(使ON在∠AOC的外部),图4(使ON在∠AOC的内部)请分别探究∠AOM与∠NOC之间的数量关系,并说明理由.
相关试题

