【题目】如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=-![]() x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.点P是y轴上一点.
x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.点P是y轴上一点.

(1)写出下列各点的坐标:点A( , )、点B( , )、点C( , );
(2)若S△COP=S△COA,请求出点P的坐标;
(3)当PA+PC最短时,求出直线PC的解析式.
参考答案:
【答案】(1)A(6,0),B(0,3),C(2,2);(2) P(0,![]() );(3)直线PC的解析式为
);(3)直线PC的解析式为![]()
【解析】
(1)x=0代入![]() ,即可求出点A坐标,把y=0代入
,即可求出点A坐标,把y=0代入![]() 即可求出点B坐标,求方程组
即可求出点B坐标,求方程组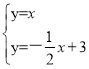 的解即可求出点C的坐标;
的解即可求出点C的坐标;
(2)设P点坐标为(0,y),根据S△COP=S△COA列方程求解即可,
(3)作点C关于y轴的对称点为M(﹣2,2),求出过点A,M的直线解析式,再求直线AM与y轴的交点坐标,即求出P的坐标,即可求出直线PC的解析式.
(1)把x=0代入![]() ,
,
∴y=3,∴B(0,3),
把y=0代入![]() ,∴x=6,A(6,0),
,∴x=6,A(6,0),
且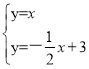 ,∴C点坐标为(2,2),
,∴C点坐标为(2,2),
(2)∵A(6,0),C(2,2)∴S△COA,=6×2÷2=6;
∵P是y轴上一点,∴设P的坐标为(0,y),
∴S△COP=![]() ,∵S△COP=S△COA,
,∵S△COP=S△COA,
∴![]() =6,∴y=±6,
=6,∴y=±6,
∴P(0,6)或(0,﹣6).
(3)如图,过点C作y轴的对称点M,连接AM与y轴交与点P,则此时PA+PC最短,

∵C的坐标为C(2,2),∴点C关于y轴的对称点为M(﹣2,2),
∴过点A,M的直线解析式为 ![]() ,
,
∵直线AM与y轴的交点为P(0,![]() ),
),
∴当P点坐标为(0,![]() )时,PA+PC最短,
)时,PA+PC最短,
∴直线PC的解析式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将半径为
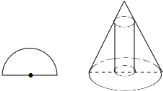
 的半圆围成一个圆锥,在圆锥内接一圆柱(如图)当圆柱的侧面的面积最大时,圆柱的底面半径是________
的半圆围成一个圆锥,在圆锥内接一圆柱(如图)当圆柱的侧面的面积最大时,圆柱的底面半径是________ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 、
、 是两条垂直的公路,设计时想在拐弯处用一段圆弧形弯道把它们连接起来(圆弧在
是两条垂直的公路,设计时想在拐弯处用一段圆弧形弯道把它们连接起来(圆弧在 、
、 两处分别与道路相切),测得
两处分别与道路相切),测得 米,
米, .
. 在图中画出圆弧形弯道的示意图(用尺规作图,保留作图痕迹,不写作法与证明);
在图中画出圆弧形弯道的示意图(用尺规作图,保留作图痕迹,不写作法与证明); 计算弯道部分的长度(结果用
计算弯道部分的长度(结果用 表示并保留根号).
表示并保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级有600名学生,在体育中考前进行了一次模拟体测.从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:
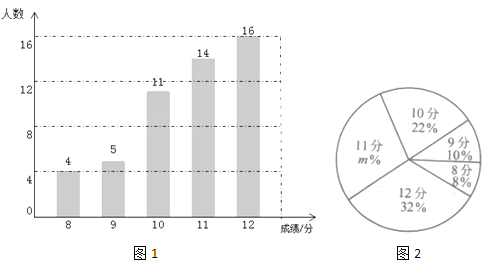
(Ⅰ)本次抽取到的学生人数为 ,图2中
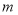 的值为 ;
的值为 ;(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级模拟体测中得12分的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 内接于
内接于 ,过点
,过点 作直线
作直线 ,
, 为非直径的弦,且
为非直径的弦,且 是
是 的切线
的切线 求证:
求证: ;
; 若
若 ,
,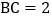 ,连接
,连接 并延长交
并延长交 于点
于点 ,求由弧
,求由弧 、线段
、线段 和
和 所围成的图形的面积.
所围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
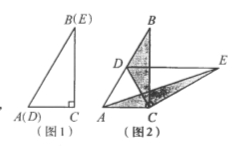


(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】建立模型:
如图1,等腰Rt△ABC中,∠ABC=90°,CB=BA,直线ED经过点B,过A作AD⊥ED于D,过C作CE⊥ED于E.则易证△ADB≌△BEC.这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角∠ABC转化为横平竖直的线段和直角,所以在平面直角坐标系中被大量使用.

模型应用:
(1)如图2,点A(0,4),点B(3,0),△ABC是等腰直角三角形.
①若∠ABC=90°,且点C在第一象限,求点C的坐标;
②若AB为直角边,求点C的坐标;
(2)如图3,长方形MFNO,O为坐标原点,F的坐标为(8,6),M、N分别在坐标轴上,P是线段NF上动点,设PN=n,已知点G在第一象限,且是直线y=2x一6上的一点,若△MPG是以G为直角顶点的等腰直角三角形,请直接写出点G的坐标.
相关试题

