【题目】如图,在![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
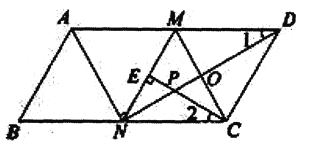
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)AN的长为2![]() .
.
【解析】
(1)利用平行四边形的性质及中点的性质即可证得结论;
(2)先判定四边形CDMN是平行四边形,再判断其为菱形,利用菱形的性质,判断△MNC为等边三角形,从而求得∠1=∠2=∠MND=30°,在![]() 中,利用特殊角,求出EN,进而求出线段AN的长.
中,利用特殊角,求出EN,进而求出线段AN的长.
(1)在平行四边形ABCD中,∠B=∠ADC,AB=CD,
∵M,N分别是AD,BC的中点,
∴BN=![]() BC=
BC=![]() AD=DM,
AD=DM,
∴△ABN ≌△CDM;
(2)∵在平行四边形ABCD中,M,N分别是AD,BC的中点,
∴![]() ,
,![]() ,
,
∴四边形CDMN为平行四边形,
∵在![]() 中,M为AD中点,
中,M为AD中点,
∴ MN=MD,
∴平行四边形CDMN为菱形;
∴∠MND=∠DNC=∠1=∠2,
∵CE⊥MN,∠MND+∠DNC+∠2=90°,
∴∠MND=∠DNC=∠2=30°,
在![]() 中,∵PE=1,∠ENP=30°,
中,∵PE=1,∠ENP=30°,
∴EN=![]() ,
,
在![]() 中,∵EN=
中,∵EN=![]() ,∠2=30°,
,∠2=30°,
NC=2 EN =2![]() ,
,
∵∠MNC=∠MND+∠DNC=60°,
∴△MNC为等边三角形,又由(1)可得,MC=AN,
∴AN=MC=NC=2![]() ,
,
∴AN的长为2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,D、E是BC边上的点,连接AD、AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)求证:△ABD≌△ACD′;
(2)如图2,若∠BAC=120°,探索BD,DE,CE之间满足怎样的数量关系时,△CD′E是正三角形;
(3)如图3,若∠BAC=90°,求证:DE2=BD2+EC2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
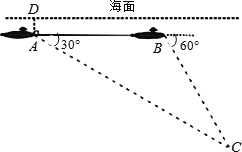
A. 2000米 B. 4000米 C. 2000米 D. (2000
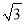 +500)米
+500)米 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )
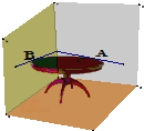
A. 45° B. 135° C. 45°或135° D. 90°或135°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
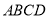 中,
中,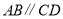 ,再添加下列其中一个条件后,四边形
,再添加下列其中一个条件后,四边形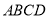 不一定是平行四边形的是( )
不一定是平行四边形的是( )A.
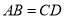 B.
B.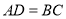 C.
C.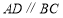 D.
D.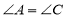
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和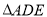 都是等边三角形,
都是等边三角形,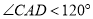 ,点
,点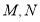 分别是
分别是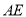 ,
, 的中点,连结
的中点,连结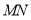 ,
,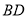 ,当
,当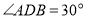 ,
,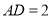 ,
,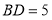 时,
时,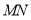 的长度为__________.
的长度为__________.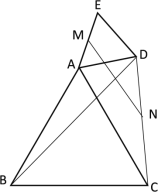
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
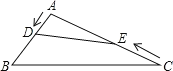
A. 4或4.8 B. 3或4.8 C. 2或4 D. 1或6
相关试题

